Kezdőlap


Feladat:	Pontversenyen kívüli P.11	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Beck József , Göndőcs Ferenc , Martoni Viktor , Somorjai Gábor
Füzet:	1969/október, 66 - 69. oldal		PDF \| MathML
Témakör(ök):	Körök, Négyszögek szerkesztése, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1968/november: Pontversenyen kívüli P.11

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen $A B C D$ a feltételeknek megfelelő húrnégyszög, adott az $A B = a$ , $B C = b$ , $C D = c$ , $D A = d$ hosszúság. Ahhoz, hogy ezekből négyszöget lehessen szerkeszteni, a legnagyobbnak is kisebbnek kell lennie a másik három összegénél.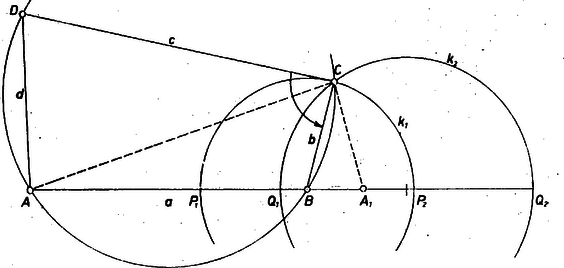
Tudjuk, hogy az $A B C D$ konvex négyszög akkor és csak akkor húrnégyszög, ha benne a szemközti szögek összege $180^{\circ}$ , ha tehát pl. a $B C$ oldal és $A B$ meghosszabbítása közti külső szög egyenlő a $C D A ∢$ -gel. Ekkor el tudunk helyezni a $C D A ▵$ -höz hasonló $C B A_{1} ▵$ -et úgy, hogy $A_{1}$ az $A B$ meghosszabbításán legyen, és a csúcsok a felsorolás sorrendjében feleljenek meg egymásnak. Ekkor a két háromszögben a megfelelő távolságok aránya $C B / C D = b / c$ . ( $A C D A ▵$ -et egy ilyen arányban és $D C B ∢$ -gel történő forgatva nyújtás viszi át a $C B A_{1} ▵$ -be.)

1. ábra

Így (1. ábra)

\begin{matrix} B A_{1} = d \frac{b}{c} . \end{matrix}

Ez a távolság ismert módon szerkeszthető, így az

\begin{matrix} A A_{1} = a + \frac{b d}{c} = \frac{a c + b d}{c} \end{matrix}

távolság, és ezen az

A

-tól a távolságra levő

B

pont is.
A

C

pont

B

-től

b

távolságra van,

A_{1}

-től és

A

-tól való távolságának aránya pedig

C A_{1} / C A = b / c

. Így

C

mint a

B

közepű,

b

sugarú

k_{1}

kör, és az

A_{1}

és

A

pontokhoz és a

b / c

arányhoz tartozó

k_{2}

Apollóniosz-kör metszéspontja adódik; az utóbbi helyett,

b = c

esetén,

A A_{1}

felező merőlegese veendő. Elég az egyik metszéspontot venni, mert a másik az

A A_{1}

-re szimmetrikus négyszöget ad.
Végül mérjük rá

A C

-re az

A C

egyenes ellenkező partján, mint amelyiken

B

van,

C

-ben az

A_{1} C B ∢

-et,

A

-ban pedig a

C A_{1} B ∢

-et, száraik metszéspontja

D

.
Az

A B C D

négyszög, ha létrejön, megfelel a feltételeknek, mert konvex, továbbá

A D C ▵ \sim A_{1} B C ▵

, mert megfelelő szögeik egyenlők, tehát

\begin{matrix} A D = \frac{A C}{A_{1} C} \cdot A_{1} B = \frac{c}{b} \cdot d \cdot \frac{b}{c} = d, C D = \frac{A C}{A_{1} C} \cdot C B = \frac{c}{b} \cdot b = c, \end{matrix}

és

A B = a

B C = b

a szerkesztés szerint. Ugyancsak az

A D C

és

A_{1} B C ▵

-ek hasonlóságából következik, hogy

A D C ∢ = A_{1} B C ∢ = 180^{\circ} - A B C ∢

, tehát a kapott négyszög húrnégyszög.
A szerkeszthetőség feltétele az, hogy a

k_{1}

és

k_{2}

köröknek legyen metszéspontjuk. Legyen a

k_{1}

körnek az

A A_{1}

egyenesen levő két metszéspontja

P_{1}

és

P_{2}

(

P_{1}

van

A

-hoz közelebb), a

k_{2}

körnek

A A_{1}

-en levő metszéspontjai pedig

Q_{1}

és

Q_{2}

(

Q_{1}

van

A

-hoz közelebb). Tegyük fel, hogy

c > b

, ekkor

k_{2}

középpontja az

A A_{1}

szakasz

A_{1}

-en túli meghosszabbításán van.

k_{1}

középpontja viszont,

B

, az

A A_{1}

szakasz belső pontja, ezért

k_{1}

-nek és

k_{2}

-nek akkor és csak akkor van (két) metszéspontja, ha

P_{1}

Q_{1}

P_{2}

Q_{2}

ebben a sorrendben követik egymást, vagyis ha teljesül az

\begin{matrix} A P_{1} < A Q_{1} < A P_{2} < A Q_{2} \end{matrix}

egyenlőtlenség (

A P_{1}

-et szükség esetén előjellel együtt értve).
Könnyen látható, hogy ez az oldalak közti

\begin{matrix} a - b < \frac{a c + b d}{b + c} < a + b < \frac{a c + b d}{c - b} \end{matrix}

egyenlőtlenség teljesülését követeli. Mármost egyszerű számítás mutatja, hogy ez akkor és csak akkor teljesül, ha az

a

d

c

oldal mindegyike kisebb a többi három adott oldal összegénél (

A P_{1} < A Q_{1}

,-ből az

a

oldal, s í. t.), ekkor pedig még inkább áll ez

b

-re. A

b = c

eset hasonló átgondolását az olvasóra hagyjuk.
E feltételek teljesülése és az oldalak sorrendjének megadása esetén a feladatnak egy megoldása van. (Természetesen, ha az oldalak sorrendjét nem írtuk elő, akkor a megoldások száma nőhet, megegyezik a szakaszokból képezhető, lényegesen különböző sorrendek számával.)

Martoni Viktor (Veszprém, Lovassy L. Gimn., II. o. t.)

II. megoldás. Abban az esetben, ha a négyszög mindkét szemben fekvő oldalpárja egyenlő, a húrnégyszög téglalap, ami könnyen megszerkeszthető. Az ellenkező esetben van olyan két szemközti oldala, melyek meghosszabbításai metszik egymást; az általánosság megszorítása nélkül feltehetjük, hogy az

A B

és

C D

oldalak ilyenek, legyen a metszéspontjuk

E

(2. ábr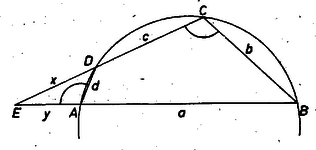a).

2. ábra

Könnyű belátni, hogy

b > d

, vagy

d > b

aszerint, hogy

E

A

, ill. a

B

csúcshoz van közelebb; feltesszük, hogy

b > d

E A D

és

E C B

hasonló háromszögek, hiszen

E

-nél közös szögük van, továbbá

E A D ∢ = E C B ∢

, mivel mindkettő a

D A B ∢

kiegészítő szöge. Bevezetve az

E A = y

és

E D = x

jelöléseket,

\begin{matrix} \frac{y}{x + c} = \frac{d}{b} és \frac{y}{x} = \frac{x + c}{y + a}, \end{matrix}

ahonnan az egyetlen pozitív megoldás:

\begin{matrix} x = d \cdot \frac{a b + c d}{b^{2} - d^{2}}, y = d \cdot \frac{a d + b c}{b^{2} - d^{2}}, \end{matrix}

két ismert módon megszerkeszthető szakasz. Ezekből megszerkesztve az

E A D ▵

-et az

E A

oldal

A

-n túli meghosszabbítására felmérjük az

A B = a

szakaszt, majd

B

-ben a

B E

félegyenesre, a

D

-t tartalmazó oldalon az

A D E ∢

-et és az új szárnak az

E D

egyenessel való metszéspontját

C

-vel jelöljük. Így

E B C ▵ \sim E D A ▵

, és ezért az

A B C D

négyszög oldalai :

\begin{matrix} B C = D A \cdot \frac{y + a}{x} = b, \\ C D = E A \cdot \frac{B C}{D A} - E D = y \cdot \frac{b}{d} - x = c, \end{matrix}

végül

D A = d

A B = a

. Másrészt az

A B C D

négyszög húrnégyszög, mert

\begin{matrix} A B C ∢ + A D C ∢ = E D A ∢ + A D C ∢ = 180^{\circ}, \end{matrix}

tehát

A B C D

megfelel a feladat követelményeinek.
A szerkeszthetőség egyetlen feltétele, hogy az

E A D ▵

létrejöjjön, mert így

B

és

C

mindig ‐ éspedig egyértelműen ‐ megszerkeszthetők. A háromszög létrejön, ha

x + y > d

x + d > y

és

y + d > x

, amiből egyszerű számítással arra jutunk, hogy rendre

b

c

a

nagyobb legyen a többi három oldal összegénél. (Ekkor pedig ugyanez

d

-re is teljesül.)

Somorjai Gábor (Budapest, I. István Gimn., III. o. t.)

III. megoldás. A II. megoldást úgy módosítjuk, hogy az

x

y

szakaszoknál egyszerűbben megszerkeszthető szakaszokat kelljen felhasználnunk. Az ottani jelöléseket tovább használjuk.
Tekintsük azt a hasonlósági transzformációt, amely az

E B C ▵

-et az

E D A ▵

-be viszi át (tükrözés a

B E C ∢

szögfelezőjére és kicsinyítés

d / b

arányban). Vigye át ez az

E D A ▵

-et az

E G F ▵

-be (vagyis az

A

B

C

D

pontot rendre az

F

D

A

G

po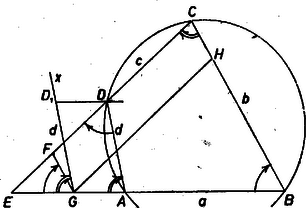ntba).

3. ábra

Ekkor egyrészt (3. ábra)

\begin{matrix} \frac{F D}{A B} = \frac{G A}{D C} = \frac{A D}{C B} (= \frac{d}{b}) = \frac{F G}{A D}, azaz \\ F D = \frac{a d}{b}, G A = \frac{c d}{b}, F G = \frac{d^{2}}{b}, \end{matrix}

másrészt

G F | | B C

, mert az

E G F ∢

-gel való elfordulás irány és nagyság szerint egyenlő az

A D E ∢

elfordulással, ez pedig az

A B C ∢

-nyi elfordulással.
Ezek szerint a

B C F G

négyszög trapéz, egy oldala adott, és további három oldalának hosszát megszerkeszthetjük. Így magát a trapézt is, abból pedig a keresett négyszöget.
Ha ugyanis

H

B C

szakasznak az a pontja, amelyre

G H | | F C

, akkor

\begin{matrix} G H = F C = F D + D C = \frac{a d}{b} + c, G B = G A + A B = \frac{c d}{b} + a \\ B H = B C - F G = b - \frac{d^{2}}{b} . \end{matrix}

Ezekből megszerkesztve a

G B H ▵

-et, a

B H

félegyenesre felmérve

B C = b

-t, a

C

-n átmenő,

H G

-vel párhuzamos egyenesből

B C

kimetszi

E

-t, a

G

-n át

B H

-val párhuzamosan húzott egyenes

F

-et. Mérjük fel ezután a

G

pontban a

B C E ∢

-gel egyenlő és megegyező irányú

E G X

szöget és a

G X

szárra a

G D_{1} = d

szakaszt, ekkor a

D_{1}

-en átmenő,

E B

-vel párhuzamos egyenes

E C

-ből kimetszi a

D

csúcsot, az ezen átmenő,

D_{1} G

-vel párhuzamos egyenes pedig

E B

-ből az

A

csúcsot.
Így egyrészt

A B C D

húrnégyszög, mert

A

-nál levő külső szöge egyenlő a

C

-nél levő szögével, egyszersmind az

E F G

szöggel, tehát másrészt az

E

-nél közös szögű

E G F

E D A

és

E B C ▵

-ek hasonlók, és mivel

G F = B C - B H = d^{2} / b

, azért

G F : D A = D A : B C = d / b = 1 / λ

, tehát ugyanaz a hasonlósági transzformáció viszi át az

E G F ▵

-et az

E D A ▵

-be, mint

E D A

-t az

E B C ▵

-be (vagyis a

G

F

D

A

pontnégyest

D

A

B

C

-be). A transzformáció az első négyes további szakaszait is a

λ

-szorosukra nyújtja:

A B = λ \cdot F D

D C = λ \cdot G A

, ezért az

A B

D C

szakaszokra fennáll:

\begin{matrix} G A + A B = \frac{D C}{λ} + A B = G B = \frac{c}{λ} + a, \\ F D + D C = \frac{A B}{λ} + D C = F C = G H = \frac{a}{λ} + c . \end{matrix}

Az elsőből, majd a másodikat is felhasználva

\begin{matrix} A B - a = \frac{1}{λ} (c - D C) = \frac{1}{λ^{2}} (A B - a), \end{matrix}

és mivel

λ > 1

A B = a

és

D C = c

. Tehát az

A B C D

négyszög az, amit szerkesztenünk kellett.