Kezdőlap


Feladat:	Pontversenyen kívüli P.8	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Beck József , Martoni Viktor , Somorjai Gábor , Szalontai Árpád , Váli László
Füzet:	1969/április, 165 - 168. oldal		PDF \| MathML
Témakör(ök):	Négyszögek szerkesztése, Pontversenyen kívüli probléma
Hivatkozás(ok):	Feladatok: 1968/október: Pontversenyen kívüli P.8

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megkísérlünk egy a kerülettel összefüggő távolságot feltüntetni az ábrán. Legyen a keresett trapéz $A B C D$ $(A B ∥ C D)$ , $D A B ∢ = α$ , $A B C ∢ = β$ az adott szögek és $A C = e$ az adott átló. Az $E F$ középvonal hossza $(A B + C D) / 2$ és ez a $G$ felezőpontjában metszi $A C$ -t. Ha még felmérjük $E F$ meghosszabbításaira az $E H = A D / 2 = E A$ és $F J = B C / 2 = F C$ szakaszokat, akkor a $H J$ szakasz hossza a kerület fele (1. ábra).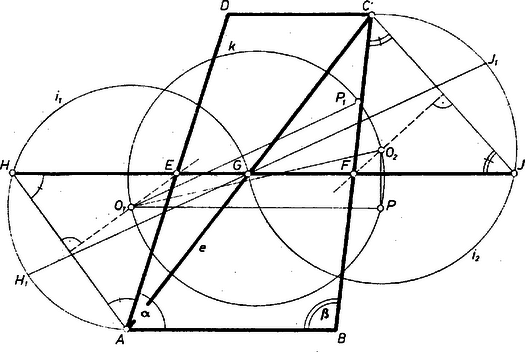

1. ábra

A C

átló felére támaszkodó

A H G

és

C J G

háromszögekben egy-egy szöget is ismerünk, ugyanis az

A E H

egyenlő szárú háromszög

E

-nél levő külső szöge

180^{\circ} - α

nagyságú, így

A H G ∢ = 90^{\circ} - α / 2

hasonlóan

C J G = β / 2

. Ezek szerint

H

A G

feletti,

90^{\circ} - α / 2

látószögű köríven van,

J

pedig a

G C

-hez tartozó

β / 2

látószögű köríven. Mivel

H

és

J

A C

egyenes ellenkező partján van, elég egy-egy látószögkörívet megrajzolni az

A C

egyenes ellenkező partjain. Legyen a két körív középpontja

O_{1}

, ill.

O_{2}

. Ezek merőleges vetülete

H J

-n egy

H J / 2 = k / 4

hosszúságú szakaszt határoz meg.

O_{1}

merőleges vetületét az

O_{2}

-ből

H J

-re bocsátott merőlegesen

P

-vel jelölve, ez az

O_{1} O_{2}

átmérőjű körön van, és

O_{1} P

hossza is

k / 4

.
Ezek alapján a következő szerkesztésre jutunk:
1. Egy

e

hosszúságú

A C

szakasznak megszerkesztjük a

G

felezőpontját és

A G

, ill.

G C

fölé az egyenes ellenkező oldalán egy

90^{\circ} - α / 2

, ill. egy

β / 2

látószögű,

i_{1}

, ill.

i_{2}

körívet; középpontjaik legyenek

O_{1}

, ill.

O_{2}

.
2. Az

O_{1} O_{2}

átmérőjű

k_{0}

kört elmetsszük az

O_{1}

körüli

k / 4

sugarú körrel. A metszéspontok legyenek (ha

k / 4 < O_{1} O_{2}

)

P

és

P_{1}

. Ha

O_{1} O_{2} = k / 4

, akkor

O_{2}

tekintendő

P

-nek, ha

O_{1} O_{2} > k / 4

, akkor a feladatnak nincs megoldása.
3. A

G

-n át

O_{1} P

-vel (ill.

O_{1} P_{1}

-gyel) húzott párhuzamos messe még

k_{1}

-et

H

-ban (ill.

H_{1}

-ben),

k_{2}

-t

J

-ben (ill.

J_{1}

-ben).
4.

A H (A H_{1})

és

C J (C J_{1})

felező merőlegesének

H J

-vel

H_{1} J_{1}

-gyel) való metszéspontja legyen

E

, ill.

F

(

E_{1}

, ill.

F_{1}

). Ha az előbbi

H G

-re (

H_{1} G

-re), az utóbbi

G J

-re (

G J_{1}

-re) esik, akkor ezek az

A D

(

A D_{1}

), ill.

B C

(

B_{1} C

) oldalak felező pontjai. Különben a feladatnak ismét nincs megoldása.
5.

A E

(

A E_{1}

) a

C

-ből,

C F

(C F_{1})

pedig az

A

-ból

H J

-vel (

H_{1} J_{1}

-gyel) húzott párhuzamosból kimetszi

D

-t, ill.

B

-t (

D_{1}

-et, ill.

B_{1}

-et).
Az elemzés lépéseinek megfordításával könnyen látható, hogy a nyert trapéz megfelel a szerkesztés kívánalmainak. Mint láttuk, a feladatnak

2

1

vagy

0

megoldása lehet.

Váli László (Budapest, I. István Gimn. )
dolgozata alapján, egyszerűsítésekkel, kiegészítésekkel

II. megoldás. Ha

α + β = 180^{\circ}

, akkor paralelogrammát kell szerkesztenünk, ami visszavezethető a következő feladatra: szerkesszük meg a háromszöget, ha adott egy oldala, a másik két oldal összege és a köztük levő szög; ennek megoldása elég ismert, itt nem foglalkozunk vele tovább.
Ha

α + β \neq 180^{\circ}

, akkor feltehetjük, hogy

α + β < 180^{\circ}

, mert a trapéz mindegyik szöge ismert, és az egyik alapon levő két szögre ez az egyenlőtlenség teljesül.
Hagyjuk egyelőre figyelmen kívül az

A C

átlót. Megrajzolva néhány, a többi feltételeket kielégítő trapézt úgy, hogy

A B

és

A D

oldalegyenesük közös legyen: a

C

csúcsok egy egyenesen látszanak sorakozni. Ha ez a megfigyelés helyes, akkor a szerkesztés könnyen elvégezhető, ezért először megfigyelésünket igazoljuk.
Rajzoljunk

k

kerületű

A B_{0} C_{0}

háromszöget, amelyben

C_{0} A B_{0} ∢ = α

és

C_{0} B_{0} A ∢ = β

. Legyen

A B C D

egy

k

kerületű trapéz, melynek

B

és

D

csúcsa az

A B_{0}

félegyenesen, ill. az

A C_{0}

szakaszon van, és

B C ∥ B_{0} C_{0}

. Jelöljük

B_{0} C_{0}

és

C D

metszéspontját

E

-vel. Ekkor

B C = B_{0} E

, s így (2. ábra)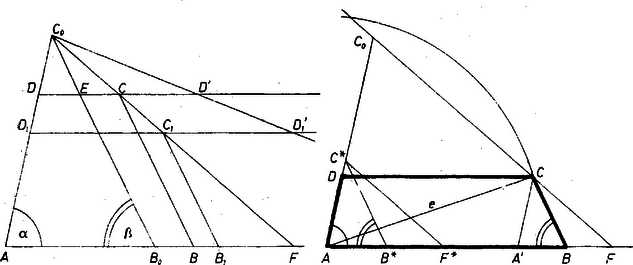

\begin{matrix} B_{0} B + C D = B_{0} B + C E + E D = 2 C E + E D = D C_{0} + C_{0} E . \end{matrix}

Eszerint ha a

D C

szakaszt meghosszabbítjuk

C

-n túl a kétszeresére, a keletkező

D D'

szakasz a

D E C_{0}

háromszög kerületével egyenlő. Ha egy másik,

k

kerületű

A B_{1} C_{1} D_{1}

trapézból indulunk ki, a

C_{0} D D'

és a megfelelő

C_{0} D_{1} D'_{1}

háromszög hasonló lesz, mert

D

-nél, ill.

D_{1}

-nél levő szögük

α

, és az ezt közrefogó oldalak aránya egyenlő (megegyezik pl. az

A B_{0} C_{0}

háromszög

A C_{0}

oldalának és kerületének az arányával).

2. ábra 3. ábra

Azt nyertük, hogy azoknak a

k

kerületű

A B C D

trapézoknak a

C

csúcsa, amelyek

A B

oldala az

A B_{0}

félegyenesen van és ezen fekvő szögeik

α

és

β

, egy a

C_{0}

-ból induló egyenesszakaszon, a

C_{0} D D'

háromszög súlyvonala egyenesének az

A_{0} B_{0}

egyenesig terjedő

C_{0} F

szakaszán van. Itt

A F

A B_{0} G_{0}

háromszög kerületének fele,

k / 2

. Meggondolásunk a következő szerkesztésre vezet:
Szerkesszünk olyan

A B^{*} C^{*}

háromszöget, amelynek

A

-nál és

B^{*}

-nál levő szöge

α

, ill.

β

, és mérjük rá

A B^{*}

-ra a háromszög kerületének felével egyenlő

A F^{*}

szakaszt, továbbá a

k / 2

hosszúságú

A F

szakaszt (3. ábra).
Az

F

-en át

F^{*} C^{*}

-gal párhuzamosan húzott félegyenest messük az

A

körüli

e

sugarú körívvel. Aszerint, hogy

2

1

vagy

0

metszéspont (ill. az érintési pont) esik az

A C^{*}

-gal való

C_{0}

metszéspont és

F

közti szakaszra, a feladatnak

2

1

0

(ill.

1

) megoldása van.
Az

A B C D

trapéz

A C

átlójának hossza

e

A

-nál és

B

-nél levő szöge

α

és

β

, azt kell még belátnunk, hogy kerülete

k

. Messe a

C

-ből

D A

-val húzott párhuzamos

A B

-t

A'

-ben, ekkor

A' B C Δ \sim A B^{*} C^{*} Δ

és

A' F C Δ \sim A F^{*} C^{*} Δ

így

\begin{matrix} A' F / A' C = A F^{*} / A C^{*} = (A B^{*} + B^{*} C^{*} + C^{*} A^{*}) / 2 A C^{*} = \\ = (A' B + B C + C A') / 2 A' C . \end{matrix}

Egy ilyen

C

metszéspontból az

A B^{*}

-gal húzott párhuzamos metszi ki

A C^{*}

-ból

D

-t a

B^{*} C^{*}

-gal húzott párhuzamos pedig

A F

-ből

B

-t.

E E' = A A' = C D

, amiből adódik, hogy a trapéz kerülete

k

. A többi tulajdonság szerkesztés szerint teljesül.

Beck József (Budapest, I. István Gimn.)
dolgozata alapján, egyszerűsítésekkel, kiegészítésekkel

Megjegyzések. 1. Egy megoldás van, ha

e

A F F_{1}

háromszög

A

-ból húzott magasságával egyenlő, vagy ha az

A E

és

A F

közül a kisebbiknél nem kisebb, de a nagyobbiknál kisebb; két megoldás van, ha a mondott magasság és kisebbik oldal közé esik, különben nincs megoldás. Ezek a távolságok kifejezhetők

α

β

és

k

segítségével, azonban a számolást itt mellőzzük.
2. A

C

pontok mértani helyét könnyen megállapíthatjuk koordináták segítségével.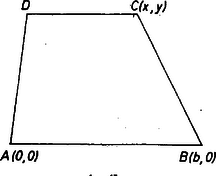

4. ábra

Legyen az

A

pont az origóban,

B

(b,0)

pont, az

A D

B C

oldalak meredeksége

m_{1}

m_{2}

. A

C

pont

(x, y)

koordinátáira keresünk összefüggést.

y

a trapéz magassága, másrészt mivel

C

B C

egyenesen van,

\begin{matrix} y = m_{2} (x - b), ahonnan b = x - \frac{y}{m_{2}}, \end{matrix}

és

D

koordinátái

(y / m_{1}, y)

. A trapéz kerülete

\begin{matrix} k = x - \frac{y}{m_{2}} + y \sqrt[]{1 + \frac{1}{m_{2}^{2}}} + x - \frac{y}{m_{1}} + y \sqrt[]{1 + \frac{1}{m_{1}^{2}}} = \\ = 2 x + y (\sqrt[]{1 + \frac{1}{m_{1}^{2}}} + \sqrt[]{1 + \frac{1}{m_{2}^{2}}} - \frac{1}{m_{1}} - \frac{1}{m_{2}}), \end{matrix}

ami valóban egyenes egyenlete. Ennek az a szakasza ad trapézt, amelyre teljesül, hogy

0 < y < m_{1} x

. (Feltettük, hogy

α

β

, egyike sem derékszög.)