Feladat: Pontversenyen kívüli P.3 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Beck József ,  Bertényi Éva ,  Csirmaz László ,  Göndőcs Ferenc ,  Reviczky János ,  Somorjai Gábor ,  Soós Miklós ,  Szabó György ,  Váli László ,  Váradi József 
Füzet: 1969/február, 72 - 74. oldal  PDF  |  MathML 
Témakör(ök): Gráfok összefüggősége, Kombinatorikus geometria, Projektív geometria, Pontversenyen kívüli probléma
Hivatkozás(ok):Feladatok: 1968/szeptember: Pontversenyen kívüli P.3

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Kíséreljünk meg megtervezni egy kívánt tulajdonságú autóbusz-hálózatot. Készítsünk táblázatot az autóbuszvonalakról, amelyeket kis betűkkel fogunk jelölni és egymás alá írunk, és a megállókról, amelyeket nagy betűkkel jelölünk és a táblázat tetején tüntetünk fel egymás után. Ha pl. az a járatnak megállója a A állomás, akkor az a sorában az A alatti mezőbe 1-est írunk, különben semmit.
Az üres táblázat ‐ hogy ti. nem közlekedik autóbusz a városban ‐, valamint az egyetlenegy járat, természetesen kielégíti az I., II., III. feltételeket, ezeket mégis figyelmen kívül hagyjuk, mivel a feladat a város autóbuszjáratairól, tehát többről szól.
Ekkor kell lennie legalább két járatnak ‐ jelöljük a-val és b-vel ‐, ezeken egy közös megállónak, A-nak, az elsőn még két megállónak, B-nek és C-nek, a másodikon két, az előbbiektől különböző megállónak, D-nek és E-nek. Így táblázatunk következő részét kapjuk:

ABCDEa111b111

Táblázatunk azonban kiegészítésre szorul, hiszen III. szerint kell lennie B-t D-vel és B-t E-vel összekötő járatnak, és ahhoz, hogy II. teljesüljön, ezek nem mehetnek át A-n, C-n, E-n, ill. A-n, C-n, D-n, és egymással sem lehet közös megállójuk B-n kívül. Így ezen a c, ill. d vonalon van egy-egy újabb F, ill. G megálló. Eddig nyert táblázatunk tehát:
ABCDEFGa111b111c111d111
 

A III. feltétel szerint kell lennie olyan járatnak, mely az A és F megállókat köti össze, jelöljük ezt e-vel. Akkor B, C, D és E nem lehetnek megállói e-nek, hiszen az ellenkező esetben e-nek és a-nak, ill. e-nek és b-nek két közös megállója lenne. Mivel e-nek és d-nek is kell, hogy közös megállója legyen, így e harmadik megállója csak G lehet.
Hasonlóan a fentiekhez, létezik olyan járat, mely C-t és D-t köti össze, jelöljük ezt f-fel. Mivel f-nek az a, b és c mindegyikével közös megállója C és D egyike, továbbá sem C, sem D nem megállója d-nek, így f harmadik megállója G.
Az eddig megadott járatok között nincs olyan, mely C-t és E-t kötné össze. Egy ilyen g járatnak C vagy E közös megállója az a, b, d járatok bármelyikével, továbbá c-nek és g-nek is kell, hogy közös megállója legyen, így F is a g járat vonalán fekszik. Egészítsük ki táblázatunkat a fentiekkel.
ABCDEFGa111b111c111d111e111f111g111

Könnyű látni, hogy táblázatunk a feladat feltételeit kielégítő hálózatot ír le. További járat nem létezhet, mert egy ilyen h járat ‐ ha további H megálló is létezik ‐ kösse össze A-t és H-t. Könnyű látni, hogy h-nak nem megállója B, C, D, E, F, G egyike sem. Viszont ekkor h-nak a c, d, f, g járatok egyikével sincs közös megállója, tehát h és H nem is létezhet. Így táblázatunk a megállók és járatok megfelelő betűzése mellett az egyetlen olyan autóbuszhálózatot reprezentálja, melyben a járatok száma egynél nagyobb. Így azt nyertük, hogy a város autóbuszjáratainak száma hét.
 

II. megoldás. Nézzük meg általánosabban, hogy hány járatra van szükség, ha az I. feltétel helyett azt kívánjuk meg, hogy
I.* minden járaton pontosan p megálló van, ahol p≥2, természetes szám.
Vizsgáljuk meg, hány megálló és autóbuszvonal lehet a városban!
Jelöljük az egyik megállóhelyen áthaladó járatok számát k-val. Mivel innen a III. feltétel szerint minden további megállóhelyre pontosan egy közvetlen járattal lehet eljutni, így I*-ból nyerjük, hogy az összes megállóhelyek száma k(p-1)+1. Ez azt is jelenti, hogy a város minden megállójában ugyanannyi (éspedig pontosan k) járat megy át. Jegyezzük meg, hogy k=0 esetén a feltételek teljesülnek, mivel ekkor nincsenek járatok, következésképpen megállóhelyek sem léteznek.
Tegyük fel a továbbiakban, hogy k≥1, s válasszunk ki egy tetszőleges járatot. A II. feltétel szerint az összes többi járat egy és csak egy pontban keresztezi ezt a járatot. Így, mivel a kiválasztott autóbuszvonal minden megállóján még további k-1 járat halad át, nyerjük, hogy az összes járatok száma p(k-1)+1.
Meghatározhatjuk a járatok számát a következőképpen is. Alkossunk párokat a város megállóhelyeiből. Ezt
[k(p-1)+1]⋅k⋅(p-1)2
-féleképpen tudjuk megtenni. Mivel minden járathoz p(p-1)2 olyan pár tartozik, amelyeket ő összeköt, s mivel III. szerint minden párt pontosan egy járat köt össze, így az összes járatok száma
[k(p-1)+1]k(p-1)p(p-1).
A kétféle meghatározás alapján felírhatjuk a
p(k-1)+1=[k(p-1)+1]⋅kp
egyenletet. Ebből átrendezéssel:
(p-1)(k-1)(k-p)=0.(1)
Mivel p≥2, így vagy k=1, vagy k=p járat megy át 1-1 megállón.
Nyilvánvaló, hogy a k=0 és k=1 triviális esethez minden p esetén létezik hálózat, mely kielégíti az I*, II. és III. feltételeket. Mivel azonban feladatunkban (ahol p≥3), a város autóbuszjáratairól szólnak a feltételek, így feltehetjük, hogy legalább két járat van, s így a fentiek szerint egyetlen megoldás lehetséges, mégpedig az, hogy 7 járat van a városban.
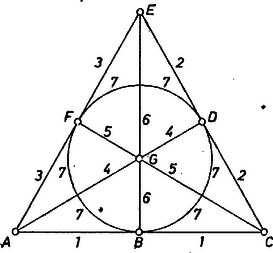
Megmutatjuk, hogy ilyen hálózat konstruálható is. Jelöljük a megállókat rendre A, B, C, D, E, F, G betűkkel, és jellemezzük a járatokat azzal a három megállóval, melyeken áthaladnak:
  az 1. számú járat az  A,   B,   C,la 2. számú járat a  1 C,   D,   E,la 3. számú járat az  E,   F,   A,la 4. számú járat az  A,   G,   D,  az 5. számú járat a  1 C,   G,   F,la 6. számú járat az  E,   G,   B,la 7. számú járat a  1 D,   F,   B  megállókon halad át.  

 

Szemléletesen mutatja ilyen hálózat létezését az ábra, ahol az 1., 2. és 3. járat egy egyenlő oldalú háromszög három oldala, a 4., 5. és 6. járat a három súlyvonal, s a 7. járat a beírt kör (lehet ennek 2/3 része is).
 

  Váradi József (Budapest, Ságvári E. Gyak. Gimn.)
 

Megjegyzés. (1) azt jelenti, hogy amennyiben van autóbuszjárat a városban, akkor csak egy vagy p2-p+1 járat lehet. Ebből azonban nem következik, hogy minden p természetes szám esetén létezik is olyan hálózat, melyben k=p.