| Feladat: | Pontversenyen kívüli P.2 | Korcsoport: 18- | Nehézségi fok: - |
| Megoldó(k): | Birkner Lajos , Csirmaz László , Fialovszky Alice , Göndőcs Ferenc , Somorjai Gábor , Soós Miklós , Váli László , Váradi József | ||
| Füzet: | 1969/február, 69 - 71. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Gyökös függvények, Egészrész, törtrész függvények, Különleges függvények, Függvényegyenletek, Pontversenyen kívüli probléma | ||
| Hivatkozás(ok): | Feladatok: 1968/szeptember: Pontversenyen kívüli P.2 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. Állítsuk elő értékét segítségével. Ezt felhasználva kapjuk, hogy II. Legyen most . Ha , akkor Ezek alapján válasszuk értékeit a következő módon: 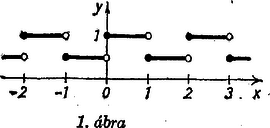 Könnyen látható, hogy a követelményeknek a következő függvény is eleget tesz (. ábra): 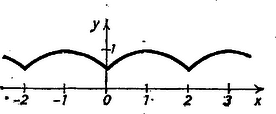 2. ábra Birkner Lajos (Budapest, Könyves Kálmán Gimn.) Soós Miklós (Budapest, Fazekas M. Gyak. Gimn.) Megjegyzés. A intervallumon értéke tetszőlegesen megadható, csak a már felhasznált , és az összefüggés értelmezhetőségét biztosító feltételeknek kell eleget tennie. Ha az helyhez az értéket rendeli hozzá a függvény, az helyen felvett függvényérték már egyértelműen meghatározott, nevezetesen 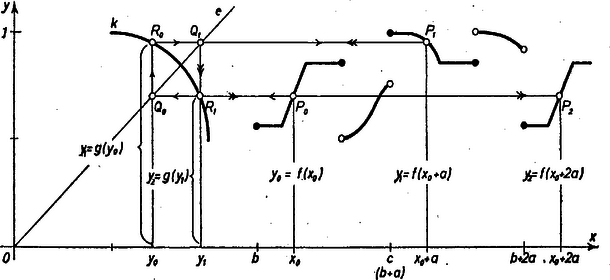 3. ábra Az függvényértéket átmásoljuk az tengelyre az origón átmenő, meredekségű egyenes segítségével, ugyanis a grafikon pontján átmenő, az tengellyel párhuzamos egyenesnek -vel való metszéspontjához tartozó abszcissza is ; így -nak a abszcisszáján levő pontjához éppen az ordináta tartozik, tehát grafikonjának az abszcissza fölötti pontját kimetszhetjük az -on át az tengellyel párhuzamosan húzott egyenessel. Hasonlóan kaptuk az abszcissza fölötti pont ordinátáját -bő] kiindulva, az ábra egymás után szerkesztett , pontjai útján. Így a feladat állítása abból következik, hogy a négyszög négyzet ‐ hiszen szimmetrikus -re ‐, és ezért , azaz . |