Kezdőlap


Feladat:	N.8	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Csörnyei Marianna , Futó Gábor , Novák A. , Pete Gábor , Szeidl Ádám
Füzet:	1994/szeptember, 308 - 309. oldal		PDF \| MathML
Témakör(ök):	Algebrai átalakítások, Geometriai egyenlőtlenségek, Terület, felszín, Számtani-mértani egyenlőtlenségek, Jensen-féle egyenlőtlenség, Egyéb sokszögek geometriája, Nehéz feladat
Hivatkozás(ok):	Feladatok: 1993/október: N.8

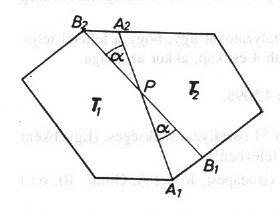
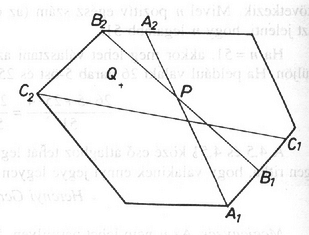
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Húzzuk meg az összes, a sokszög valamely csúcsán áthaladó és a területet felező szakaszt. Nyilvánvaló, hogy közülük bármely kettő metszi egymás a sokszög belsejében. Ellenkező esetben ugyanis az általuk és a sokszög határa által közrefogott síkidom területe nulla kell hogy legyen (hiszen területfelezőkről van szó).
Két ilyen területfelező szakaszt akkor nevezünk szomszédosnak, ha megfelelő végpontjaik szomszédosak a sokszög kerületén.

1. ábra 2. ábra

Legyenek ilyenek pl. az

A_{1} A_{2}

és

B_{1} B_{2}

szakaszok (az 1. ábra szerint). Ez nyilván azt is jelenti, hogy

A_{1}

és

B_{1}

(illetve

A_{2}

és

B_{2}

) között a sokszögnek nincs csúcsa ‐ éppen a szomszédosság miatt. Ha az

A_{1} A_{2}

és

B_{1} B_{2}

szakaszok metszéspontja

P

, az

A_{1} P B_{1}

szög pedig

α

, akkor belátjuk, hogy

\begin{matrix} T_{A_{1} P B_{1}} + T_{A_{2} P B_{2}} \leq \frac{1}{4} \cdot sin α . \end{matrix}

Vegyük észre először, hogy

T_{A_{1} P B_{1}} = T_{A_{2} P B_{2}}

, ez az

A_{1} A_{2}

és

B_{1} B_{2}

szakaszok területfelező tulajdonságából következik, amint ezt az ábra szemlélteti:

T_{A_{1} B_{1} P} = \frac{T}{2} - T_{2}, T_{A_{2} B_{2} P} = \frac{T}{2} - T_{1}

és

T_{1} = T_{2}

Ezek szerint

\begin{matrix} \frac{A_{1} P \cdot P B_{1} \cdot sin α}{2} = \frac{A_{2} P \cdot P B_{2} \cdot sin α}{2} . \end{matrix}

Innen

A_{1} P \cdot P B_{1} = A_{2} P \cdot P B_{2} .

A feladat feltétele szerint

A_{1} P + P A_{2} \leq 1

és hasonlóan

B_{1} P + P B_{2} \leq 1

. Mivel itt pozitív(nemnegatív) értékekről van szó, használhatjuk a számtani és mértani közepek közti egyenlőtlenséget:

A_{1} P \cdot P A_{2} \leq \frac{1}{4}

és

B_{1} P \cdot P B_{2} \leq \frac{1}{4} .

Összeszorzás és rendezés után:

\begin{matrix} \frac{1}{16} \geq (A_{1} P \cdot P B_{1}) (A_{2} P \cdot P B_{2}) = {(A_{1} P \cdot P B_{1})}^{2}, \end{matrix}

azaz

\begin{matrix} \frac{1}{4} \geq A_{1} P \cdot P B_{1} . \end{matrix}

Innen pedig
(1)

T_{A_{1} P B_{1}} + T_{A_{2} P B_{2}} = \frac{1}{2} sin α [A_{1} P \cdot P B_{1} + A_{2} P \cdot P B_{2}] \leq \frac{1}{4} sin α .

Ezután megmutatjuk, hogy az oly módon definiált háromszögek, mint az

A_{1} P B_{1}

és

A_{2} P B_{2}

, lefedik az egész sokszöget. Legyen a sokszög egyik belső pontja

Q

(2.ábra). Vizsgáljuk először azt, hogy

Q

A_{1} A_{2}

területfelező melyik oldalán van. Majd ezen az oldalon maradva induljunk tovább

A_{1}

-ből a sokszög kerületén, amíg egy újabb területfelező szakasz egyik végpontjához nem érünk. Most is abba az irányba menjünk tovább, amelyik oldalra

Q

esik. Látható, hogy így

Q

beszorítható két szomszédos területfelező ,,közé'', tehát valóban lefedi valamelyik kívánt alakú háromszög.
Becsüljük most az (1) segítségével az ilyen háromszögek területének összegét:

(2)

T_{sokszög} \leq \sum T_{háromszögek} \leq \frac{1}{4} (sin α_{1} + sin α_{2} + ... + sin α_{n})

Fontos észrevétel, hogy

α_{1} + α_{2} + ... + α_{n} = π

(hiszen ez úgy is felfogható, hogy az

A_{1} A_{2}

egyenest

α_{1}

, majd

α_{2}, ..., α_{n}

szögekkel forgatom el, s végül az

A_{2} A_{1}

-hez jutok.)
Mivel a szinuszfüggvény a

[0, π]

intervallumon konkáv, használhatjuk a Jensen-egyenlőtlenséget:

\begin{matrix} \frac{sin α_{1} + sin α_{2} + ... + sin α_{n}}{n} \leq sin (\frac{α_{1} + ... + α_{n}}{n}) = sin \frac{π}{n} < \frac{π}{n} . \end{matrix}

Az utolsó lépésnél kihasználtuk a pozitív

x

-ekre (és a

\frac{π}{n}

ilyen) teljesülő, ismert

sin x < x

egyenlőtlenséget. Innen:

\begin{matrix} \frac{1}{4} (sin α_{1} + ... + sin α_{n}) < \frac{π}{4} . \end{matrix}

Ez pedig (2)-vel összevetve épp a bizonyítandó állítást adja.

Szeidl Ádám (Miskolc, Földes F. Gimn., IV. o.t.)