Kezdőlap


Feladat:	N.7	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Csörnyei Marianna , Futó Gábor , Gyarmati Katalin , Hertz István
Füzet:	1994/április, 211 - 212. oldal		PDF \| MathML
Témakör(ök):	Algebrai átalakítások, Geometriai egyenlőtlenségek, Számtani-mértani egyenlőtlenségek, Koszinusztétel alkalmazása, Szögfelező egyenes, Nehéz feladat
Hivatkozás(ok):	Feladatok: 1993/október: N.7

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög oldalait és szögeit a szokásos módon $a, b, c, α, β, γ$ -val (lásd az ábrát). A szögfelezőtétel serint $C Q = \frac{a b}{a + c}$ és $C P = \frac{a b}{b + c}$ . Írjuk fel a $C Q P$ háromszögben a koszinusztételt a $P Q$ oldalra:

\begin{matrix} P Q^{2} = {(\frac{a b}{a + c})}^{2} + {(\frac{a b}{b + c})}^{2} - 2 \frac{{(a b)}^{2}}{(a + c) (b + c)} cos γ . \end{matrix}

A B C

háromszög

a

oldalára vonatkozó koszinusztételből:

\begin{matrix} cos γ = \frac{a^{2} + b^{2} - c^{2}}{2 a b} . \end{matrix}

Ezt (1)-be helyettesítve kapjuk, hogy

\begin{matrix} P Q^{2} = {(\frac{a b}{a + c})}^{2} + {(\frac{a b}{b + c})}^{2} - \frac{a b (a^{2} + b^{2} - c^{2})}{(a + c) (b + c)} . \end{matrix}

Megmutatjuk, hogy

P Q \leq A Q \cdot B P

. Ez a szögfelezőtétel és (2) szerint pontosan akkor teljesül, ha

\begin{matrix} {(\frac{a b}{a + c})}^{2} + {(\frac{a b}{b + c})}^{2} - \frac{a b (a^{2} + b^{2} - c^{2})}{(a + c) (b + c)} \leq \frac{b c}{a + c} \cdot \frac{a c}{b + c} . \end{matrix}

Az egyenlőtlenséget

a \cdot b

-vel elosztva és rendezve kapjuk, hogy

\begin{matrix} \frac{a \cdot b}{{(a + c)}^{2}} + \frac{a b}{{(b + c)}^{2}} \leq \frac{a^{2} + b^{2}}{(a + c) (b + c)} . \end{matrix}

Megszorozva

\frac{(a + c) (b + c)}{a \cdot b}

-vel:

\begin{matrix} \frac{b + c}{a + c} + \frac{a + c}{b + c} \leq \frac{b}{a} + \frac{a}{b} . \end{matrix}

Ezt rendezve pedig nyilvánvalóan az igaz

\begin{matrix} 0 \geq \frac{a {(b - a)}^{2} (a + b + c)}{a \cdot b \cdot (a + c) (b + c)} \end{matrix}

egyenlőséget kapjuk.
A számtani és a mértani közép közti egyenlőtlenség alapján

\sqrt[]{A Q \cdot B P} \leq \frac{A Q + B P}{2}

, vagyis

P Q \leq \frac{A Q + B P}{2}

. Ugyanígy láthatjuk be, hogy

Q R \leq \frac{C Q + R B}{2}

és

R P \leq \frac{A R + P C}{2}

. E három egyenlőtlenséget összeadva éppen a bizonyítandó állítást kapjuk.

Hanyecz Péter, Budapest

Megjegyzés. A példa F.2977. feladatnak a nehezebben megoldható ,,párja''.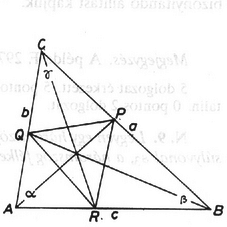