Feladat: N.6 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Braun Gábor ,  Burcsi Péter ,  Csörnyei Marianna ,  Dombi Gergely ,  Futó Gábor ,  Gyarmati Katalin ,  Hertz István ,  Koblinger Egmont ,  Németh Ákos ,  Németh Zoltán ,  Novák András ,  Pap Gyula 
Füzet: 1994/április, 210 - 211. oldal  PDF  |  MathML 
Témakör(ök): Sakktáblával kapcsolatos feladatok, Bolyongási feladatok, Nehéz feladat
Hivatkozás(ok):Feladatok: 1993/október: N.6

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Bebizonyítjuk, hogy ha m és n közül legalább az egyik páros, akkor a kezdőnek, ha pedig m és n páratlan, akkor a második játékosnak van nyerő stratégiája.
Vizsgáljuk először azt az esetet, amikor m és n közül valamelyik páros. A szimmetria miatt feltehetjük, hogy ez m. Osszuk fel a sakktáblát 2×1 -es téglalapokra:
Most mutatunk egy olyan stratégiát, amivel a kezdő biztosan nyer.
Lépjen mindig annak a téglalapnak a másik mezőjére, ahol a király áll. Ha ezt a taktikát követi, a következőket éri el:

‐az ő lépése után minden egyes téglalapnak vagy mindkét mezőjén járt a király, vagy pedig egyiken sem;
‐a második játékosnak mindig olyan 2×1-es téglalpba kell lépnie, ahol még nem járt a király;
‐ha a másodk játékos lépett, akkor a király olyan téglalapban áll, amelynek másik mezője még szabad;

Mivel a sakktábla mezői előbb-utóbb elfogynak, a kezdő pedig mindig tud lépni, a második játékos veszít.
Most azt az esetet vizsgáljuk meg, amikor m és n páratlan.
Osszuk fel a táblának a bal felső, kiindulási mezőt nem tartalmazó részét 2×1-es és 1×2-es téglalapokra. Ezt megtehetjük úgy, hogy az első sorból megmaradó n-1 mezőt 1×2-es, a többi (m-1)×n mezőt pedig 2×1-es téglalapokra osztjuk.
Ha most a második játékos követi az előbbi stratégiát, akkor ő nyer, mert mindig a kezdőnek kell új téglalapba lépni, aminek ő rögtön rálép a másik mezőjére.
Megjegyzés. Az, hogy kinek van nyerő stratégiája, nem függ attól, hogy honnan indul a király. Az első esetben a bizonyítás szóról szóra elismételhető.
A második esetben módosítani kell a bizonyítást, mert a tábla maradék része (ha nem ugyanannyi sötét és világos mezőből áll), nem osztható fel mindig 2×1-es és 1×2-es téglalapokra. Ha viszont átlós helyzetű mezőpárokat is felhasználunk, a felosztás mindig elvégezhető.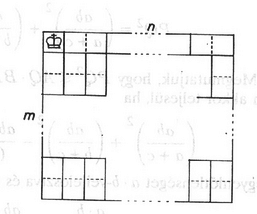