Kezdőlap


Feladat:	Gy.2890	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csordás Péter
Füzet:	1994/november, 436 - 437. oldal		PDF \| MathML
Témakör(ök):	Egyenlő szárú háromszögek geometriája, Hossz, kerület, Terület, felszín, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1994/január: Gy.2890

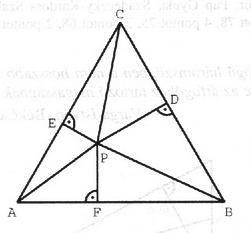
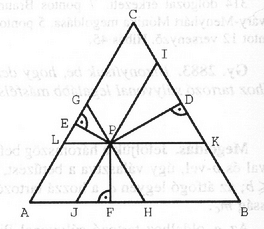
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög oldalának hosszát $a$ -val. Megmutatjuk, hogy a feladatban szereplő tört számlálója is és nevezője is csak $a$ -tól függ.
A háromszög területét kétféleképpen felírva (1. ábra)

\begin{matrix} t_{A B C} = t_{A P B} + t_{B P C} + t_{C P A}, \end{matrix}

azaz

\begin{matrix} \frac{a^{2} \sqrt[]{3}}{4} = \frac{a \cdot P F}{2} + \frac{a \cdot P D}{2} + \frac{a \cdot P E}{2} . \end{matrix}

Ebből a tört számlálójára

P D + P E + P F = \frac{a \sqrt[]{3}}{2}

adódik.
Húzzunk

P

-n át párhuzamosokat az

A B C

háromszög oldalaival, s jelöljük ezeknek az egyeneseknek a háromszög oldalával való metszéspontjait a 2. ábrán látható módon. Az

A B K L

B C G H

és

C A J I

négyszögek szimmetrikus trapézok,ezért

A L = B K

B H = C G

és

A J = C I

. A

P J H

P K I

, és

P G L

háromszögek minden szöge 60

^{\circ}

, ezért ezek szabályos háromszögek, amelyekben

P F

P D

és

P E

oldalfelező merőlegesek. Ezek alapján az

A B C

háromszög kerületét a következő alakban írhatjuk:

\begin{matrix} 3 a = (A J + J F + F H + H B) + (B K + K D + D I + I C) + (C G + G E + E L + L A) = \\ = [(A J + J F) + (I C + F H)] + [(B K + K D) + (A L + D I)] + [(C G + G E) + (H B + E L)] = \\ = 2 (A F + B D + C E) . \end{matrix}

Vagyis

A F + B D + C E = \frac{3 a}{2} .

Tehát a keresett tört értéke:

\begin{matrix} \frac{P D + P E + P F}{B D + C E + A F} = \frac{\frac{a \sqrt[]{3}}{2}}{\frac{3 a}{2}} = \frac{\sqrt[]{3}}{3} . \end{matrix}

Csordás Péter (Kecskemét, Zrínyi I. Ált. Isk., 8. o. t.)