Kezdőlap


Feladat:	Gy.2883	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bérczi Gergely , Burcsi Péter , Elek Péter , Fejes Tóth Péter , Fejős Ibolya , Hosszú Zsolt , Kiss Márton , Muth Lóránt , Pap Gyula
Füzet:	1994/november, 435 - 436. oldal		PDF \| MathML
Témakör(ök):	Nevezetes azonosságok, Geometriai egyenlőtlenségek, Derékszögű háromszögek geometriája, Súlyvonal, Magasságvonal, Gyakorlat
Hivatkozás(ok):	Feladatok: 1993/december: Gy.2883

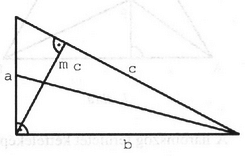
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög befogóit $a$ -val és $b$ -vel, úgy választva a betűzést, hogy $a \leq b$ ; az átfogó legyen $c$ , a hozzá tartozó magasság $m_{c}$ .
Az $a$ oldalhoz tartozó súlyvonal Pitagorasz tétele szerint $\sqrt[]{b^{2} + \frac{a^{2}}{4}}$ . A háromszög területét kétféleképpen felírva kapjuk, hogy $\frac{1}{2} a b = \frac{1}{2} c m_{c}$ , vagyis $m_{c} = \frac{a b}{c} = \frac{a b}{\sqrt[]{a^{2} + b^{2}}}$ . Bizonyítandó állításunk tehát így írható:

\begin{matrix} \sqrt[]{b^{2} + \frac{a^{2}}{4}} \geq \frac{3}{2} \cdot \frac{a b}{\sqrt[]{a^{2} + b^{2}}} . \end{matrix}

Négyzetre emelve és rendezve:

\begin{matrix} (4 b^{2} + a^{2}) (a^{2} + b^{2}) \geq 9 a^{2} b^{2} . \end{matrix}

Tovább alakítva:

\begin{matrix} 4 b^{4} + a^{4} - 4 a^{2} b^{2} = {(2 b^{2} - a^{2})}^{2} \geq 0. \end{matrix}

Mivel ez az egyenlőtlenség nyilván teljesül, és ekvivalens átalakításokat végeztünk, azért a feladat állítását bebizonyítottuk.
Megjegyzés. A megoldás során nem használtuk fel, hogy

a \leq b

, tehát az állítás mindkét befogóhoz tartozó súlyvonal esetén igaz.

Kiss Márton (Fazekas M. Főv. Gyak. Gimn., II. o. t.) dolgozata alapján