Feladat: Gy.2857 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1994/április, 189 - 190. oldal  PDF  |  MathML 
Témakör(ök): Részhalmazok, Halmazok számossága, Gyakorlat
Hivatkozás(ok):Feladatok: 1993/szeptember: Gy.2857

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatot a következő állítás segítségével fogjuk megoldani:

Ha egy iskolában a három nyelv mindegyikét pontosan 2n-en beszélik, akkor kiválasztható közülük néhány tanuló úgy, hogy közülük pontosan 2 beszélje az egyes nyelveket.

Ez valóban elegendő, hiszen ezt az állítást alkalmazva 2n=50-nel, majd a megmaradtakra 2n=48-cal és így tovább, majd a létrejött 25 csoportot ötösével összefogva, a kívánt tulajdonságú csoportokat kapjuk. Mivel azok, akik egyik nyelvet sem beszélik, bárhová beoszthatók, azért feltehető, hogy ilyenek nincsenek is.
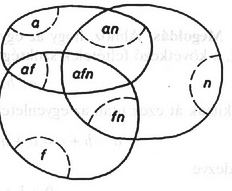
Jelölje a csak angolul tudók halmazát a, számát Na; hasonlóan értelmezzük az f,n,an,af,fn,afn halmazokat és az Nf,Nn,Naf,Nfn,Nafn számokat. A szétosztást a következő esetekre lebontva végezzük:

1.Naf≠0,Nan≠0,Nfn≠0. Ekkor egy af-beli, egy an-beli és egy fn-beli gyerek megfelel.
2.Naf=0,Nan≠0,Nfn≠0. Ekkor látható, hogy Nafn+Nan+Na gyerek tud angolul, míg németül Nn+Nfn+Nan+Nafn, azaz Nafn+Nan+Na=Nn+Nafn+Nan+Nfn>Nn+Nafn+Nan≤Nafn+Nan, amiből Na≤1. Hasonlóan Nf≤1, így egy an-beli, egy fn-beli, egy a-beli és egy f-beli megfelel.
3.Nfn≠0,Nafn≠0,Nan=Naf=0. Ekkor angolul Na+Nafn gyerek beszél, németül pedig Nfn+Nafn+Nn, vagyis Na+Nafn=Nn+Nafn+Nfn>Nafn, azaz Na≥1. Ekkor egy a-beli, egy fn-beli lesz jó.
4.Nfn≠0,Nafn=Nan=Naf=0.
a)Nfn≥2. Ilyenkor angolul Na gyerek tud, azaz Na=2n≥2, s így két a-beli és két fn-beli megfelel.
b)Nfn=1. Ekkor szintén Na≥2, valamint a németül tudók számára 2n=Nfn+Nn=1+Nn, amiből Nn>1, választhatunk tehát két a-belit, egy-egy n-, f és fn-belit.
5.Nan=Naf=Nfn=0.
a)Nafn≥2. Ekkor válasszunk két afn-belit.
b)Nafn=1. A 4.b) esethez hasonlóan látható, hogy ekkor Na≥1,Nn≥1,Nf≥1, azaz választhatunk egy-egy afn-,a-, és f-belit.
c)Nafn=0. Ekkor Na=2n≥2,Nf≥2,Nn≥2; vegyünk e három halmazból 2-2 gyereket.

Mivel az egyes nyelvek szerepe felcserélhető, azért az összes esetet felsoroltuk: ha az Naf,Nfn,Nan egyike sem 0; egyikük 0; kettő 0 és Nafn≠0; valamint ha mindhárom 0. Ezzel beláttuk segédállításunkat, s az elején mondottak szerint a feladatot is megoldottuk.