Kezdőlap


Feladat:	Gy.2781	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1993/január, 21 - 22. oldal		PDF \| MathML
Témakör(ök):	Konstruktív megoldási módszer, Térelemek és részeik, Tetraéderek, Vektorok lineáris kombinációi, Alakzatok súlypontja (tömegközéppontja), Gyakorlat
Hivatkozás(ok):	Feladatok: 1992/május: Gy.2781

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $A B C D$ egy tetraéder, súlypontja $S$ , a $D$ csúcsból kiinduló éleinek felezőpontja $F_{A}$ , $F_{B}$ , $F_{C}$ , a $D$ -re illeszkedő lapok súlypontjai $K_{A}$ , $K_{B}$ , $K_{C}$ , végül a $D S$ szakasz $S$ -hez közelebbi ötödölőpontja $E$ . Megmutatjuk, hogy ehhez a $12$ ponthoz meg lehet adni $12$ , a feltételeknek megfelelő síkot.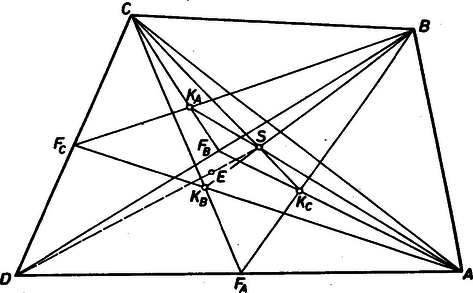

1. ábra

A súlypont definíciójából következik, hogy az (

A

K_{C}

F_{B}

); (

A

K_{B}

F_{C}

); (

B

K_{A}

F_{C}

); (

B

K_{C}

F_{A}

); (

C

K_{A}

F_{B}

); (

C

K_{B}

F_{A}

); (

A

K_{A}

S

); (

B

K_{B}

S

) és (

C

K_{C}

S

) ponthármasok kollineárisak. A

D S

F_{A} K_{A}

F_{B} K_{B}

és

F_{C} K_{C}

egyenesek mindegyike átmegy az

E

ponton. Ezt vektorok segítségével bizonyítjuk: Ha

\vec{D A} = 60 a, \vec{D B} = 60 b

és

\vec{D C} = 60 c

, akkor a felezőpont, illetve a súlypont helyvektorának ismert tulajdonsága alapján

{\vec{D F}}_{A} = 30 a

{\vec{D F}}_{B} = 30 b

{\vec{D F}}_{c} = 30 c

{\vec{D K}}_{A} = 20 (b + c)

{\vec{D K}}_{B} = 20 (a + c)

és

{\vec{D K}}_{C} = 20 (a + b)

\vec{D S} = 15 (a + b + c)

, ezért

\vec{D E} = 12 (a + b + c)

. Viszont a szakaszt adott arányban osztó pont helyvektorára vonatkozó képlet szerint a

12 (a + b + c)

vektor éppen az

F_{A} K_{A}

F_{B} K_{B}

és

F_{C} K_{C}

szakaszokat

3 : 2

arányban osztó pont helyvektora, mivel

\begin{matrix} \frac{2 \cdot 30 a + 3 \cdot 20 (b + c)}{2 + 3} = \frac{2 \cdot 30 b + 3 \cdot 20 (a + c)}{2 + 3} = \frac{2 \cdot 30 c + 3 \cdot 20 (a + b)}{2 + 3} = \\ = 12 (a + b + c) . \end{matrix}

Ezek után már könnyen megadhatjuk a feltételeknek eleget tevő

12

síkot: az eredeti tetraéder

D

-n átmenő

3

lapsíkja; az a

4

sík, amelyik a tetraéder egy

D

-n át nem menő élét és az ezzel szemközti él felezőpontját tartalmazza, továbbá átmegy a tetraédernek és két lapjának a súlypontján (ilyen sík pl. az

A

B

F_{C}

S

K_{A}

K_{B}

pontok síkja); végül az a

6

sík, amely átmegy a

D F_{A} K_{B} F_{C} F_{B} K_{C} S K_{A}

csonkagúla két-két szemközti élén, az

E

ponton és az

A

B

C

pontok egyikén (ilyen sík pl. az

F_{A}

K_{B}

F_{B}

K_{A}

E

C

pontok síkja). Ez utóbbi síkok létezésének bizonyítása azon múlik, hogy az említett csonkagúláról megmutattuk, hogy valamennyi testátlója átmegy az

A

B

C

pontok valamelyikén.
A

12

pont közül semelyik

6

nem kollienáris, ezért a

12

síkkal együtt eleget tesznek a feladat feltételeinek.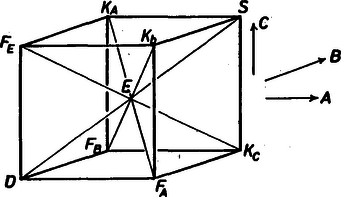

2. ábra

Megjegyzések 1. A feladatban szereplő alakzat tulajdonképpen a projektív geometriában ismert ún. Reye-féle konfiguráció. Ennek a projektív térben a legegyszerűbb előállítása a következő: a pontok egy kocka csúcsai, a kocka középpontja és a kocka három élirányának megfelelő ideális pontok; a síkok a kocka lapsíkjai és két-két szemközti élét tartalmazó síkok. A 2. ábrán jól látható az analógia megoldásunk és a kocka között.

2. Belátható, hogy négy gömb páronként vett külső és belső hasonlósági pontjai is a feladatban szereplő konfigurációt alkotják.