Kezdőlap


Feladat:	Gy.2779	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Rákóczi Bálint
Füzet:	1992/december, 447 - 449. oldal		PDF \| MathML
Témakör(ök):	Kombinatorikai leszámolási problémák, Négyzetrács geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1992/május: Gy.2779

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek a konvex sokszög csúcsai $A (5; 0)$ , $B (5; 5)$ , $C (0; 5)$ , $D$ , $...$ ; a koordináta-rendszer kezdőpontja pedig $O$ . A feltételeknek eleget tevő sokszögeket csúcsaik száma alapján számoljuk össze.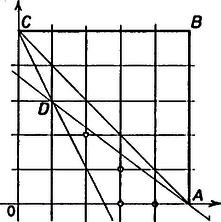
Háromszög egy van, az $A B C$ . Négyszög $A$ , $B$ , $C$ -től különböző negyedik csúcsa tetszőleges olyan rácspont lehet, amelyik az $A C O$ háromszög belsejében, vagy annak $C O$ vagy $O A$ oldalán van (1. ábra).

1. ábra

Ezeknek a pontoknak a száma 15, tehát ennyi négyszög van. Az

A B C D E

ötszög akkor felel meg a feltételeknek, ha az

E

csúcs a

C O

egyenestől jobbra ‐ az

A

-t tartalmazó félsíkban ‐ és az

A D

egyenes alatt ‐ az

O

-t tartalmazó félsíkban ‐ van.

D

választásától függően különböző számú ötszöget kapunk, ez látható a 2. ábrán.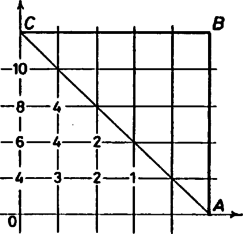

2. ábra

Összesen

10 + 8 + 4 + 6 + 4 + 2 + 4 + 3 + 2 + 1 = 44

jó ötszög van. Ugyanezzel a módszerrel számolhatjuk össze a hatszögeket ‐ 3. ábra ‐, amelyek száma 16.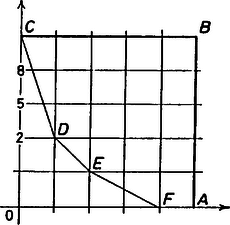

3. ábra

Hétszögből csak egy ‐ a 4. ábrán látható ‐ létezik, több csúcsú sokszög pedig nem lehet, mert akkor az

A

B

C

-től különböző legalább 5 csúcs közt vagy lenne kettő, amelyeknek első vagy második koordinátája megegyezik, s így a sokszög nem lenne konvex, vagy pedig lenne három, amelyek egy egyenesen vannak.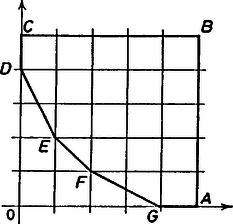

4. ábra

Összesen tehát

1 + 15 + 44 + 16 + 1 = 77

, a feltételeknek eleget tevő sokszög van.

Rákóczi Bálint (Fazekas M. Főv. Gyak. Gimn., II. o. t.) dolgozata alapján