Kezdőlap


Feladat:	Gy.2755	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Dőtsch András , György András , Hegedűs Márton , Koltai Róbert , Révai András , Székelyhidi László
Füzet:	1992/október, 306 - 307. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Vektorok skaláris szorzata, Súlyvonal, Gyakorlat
Hivatkozás(ok):	Feladatok: 1992/február: Gy.2755

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ismert, hogy egy tetszőleges háromszög oldalai és súlyvonala közt a szokásos jelöléseket használva fennáll a következő összefüggés: $c^{2} + 4 s_{c}^{2} = 2 (a^{2} + b^{2})$ . (Ennek bizonyítása megtalálható pl. a Geometriai feladatok gyűjteménye I. kötetének 1673. feladatában).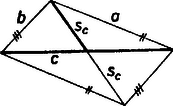

1. ábra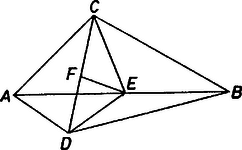

2. ábra

Legyen az

A B

szakasz felezőpontja

E

, a

C D

szakasz felezőpontja pedig

F

. A súlyvonalra vonatkozó összefüggést az

A B C

A B D

és

D E C

háromszögekre felírva:

\begin{matrix} A B^{2} + 4 C E^{2} = 2 (A C^{2} + B C^{2}), & (1) \\ A B^{2} + 4 D E^{2} = 2 (A D^{2} + B D^{2}), & (2) \\ C D^{2} + 4 E F^{2} = 2 (D E^{2} + C E^{2}) . & (3) \end{matrix}

(1)-et és (2)-t összeadva, majd ebbe helyettesítve (3)-at, kapjuk, hogy

\begin{matrix} 2 (A C^{2} + B C^{2} + A D^{2} + B D^{2}) = 2 A B^{2} + 4 (C E^{2} + D E^{2}) = 2 A B^{2} + 2 C D^{2} + 8 E F^{2} . \end{matrix}

Átrendezve:

\begin{matrix} (A B^{2} - A C^{2} - B C^{2}) + 4 E F^{2} = A D^{2} + B D^{2} - C D^{2} . \end{matrix}

Mivel az

A B C

háromszög tompaszögű, azért

A B^{2} > A C^{2} + B C^{2}

, tehát a bal oldalon álló kifejezés pozitív; ezért az egyenlőség jobb oldalán álló kifejezés is az, vagyis

A D^{2} + B D^{2} > C D^{2}

Hegedűs Márton (Nyíregyháza, 1. sz. Gyak. ÁIt. Isk., 8. o. t.)
dolgozata alapján

II. megoldás. Vektorok skaláris szorzatát használva oldjuk meg a feladatot.

\begin{matrix} {\vec{C D}}^{^{2}} \leq {\vec{C D}}^{^{2}} + {(\vec{C D} - \vec{C A} - \vec{C B})}^{2} = \end{matrix}

\begin{matrix} {\vec{C D}}^{^{2}} + {\vec{C D}}^{^{2}} + {\vec{C A}}^{^{2}} + {\vec{C B}}^{^{2}} - 2 \vec{C D} \cdot \vec{C A} - 2 \vec{C D} \cdot \vec{C B} + 2 \vec{C A} \cdot \vec{C B} = \end{matrix}

\begin{matrix} {(\vec{C D} - \vec{C A})}^{2} + {(\vec{C D} - \vec{C B})}^{2} + 2 \vec{C A} \cdot \vec{C B} = {\vec{A D}}^{^{2}} + {\vec{B D}}^{^{2}} + 2 \vec{C A} \cdot \vec{C B} . \end{matrix}

Mivel az

A B C

háromszögben

C

-nél tompaszög van, azért

\vec{C A}

\cdot

\vec{C B} < 0

, vagyis

{\vec{C D}}^{^{2}}

{\vec{A D}}^{^{2}}

{\vec{B D}}^{^{2}}

. Ez éppen a bizonyítandó állítás.

Székelyhidi László (Debrecen, Tóth Á. Gimn., I. o. t.) dolgozata alapján

Megjegyzés. A II. megoldásban nem használtuk ki, hogy a

D

pont benne van az

A B C

síkban.