Kezdőlap


Feladat:	Gy.2754	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	György András , Révai András
Füzet:	1992/október, 305 - 306. oldal		PDF \| MathML
Témakör(ök):	Egész számok összege, Kombinatorikus geometria síkban, Kombinatorikai leszámolási problémák, Kombinációk, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1992/február: Gy.2754

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a $(2 n + 1)$ -szög csúcsait $A_{0}$ , $A_{1}$ , $A_{2}$ , $...$ , $A_{2 n}$ -nel, középpontját pedig $O$ -val. Tekintsük az $A_{0} A_{k}$ átlót $(k \leq n)$ . Az $A_{0} A_{k} A_{l}$ háromszög pontosan akkor tartalmazza $O$ -t, ha $A_{l}$ az $O A_{0}$ és az $O A_{k}$ egyenesek által meghatározott négy síknegyed közül az $A_{0} A_{k}$ szakaszt tartalmazóval szemköztiben van. Az $O A_{0}$ egyenes a sokszög $A_{n} A_{n + 1}$ , az $O A_{k}$ egyenes pedig a sokszög $A_{n + k} A_{n + 1 + k}$ oldalát metszi, tehát $A_{0} A_{k} A_{l}$ pontosan akkor jó háromszög, ha $n + 1 \leq l \leq n + k$ (1. ábra). Ezért rögzített $A_{0} A_{k}$ esetén a jó háromszögek száma $(n + k) - n = k$ . Vagyis az $A_{0}$ -t tartalmazó jó háromszögek száma $1 + 2 + ... + n = \frac{n (n + 1)}{2}$ .

1. ábra

Nyilván ugyanennyi jó háromszög tartalmazza a

(2 n + 1)

-szög tetszőleges, rögzített csúcsát. Ezért

(2 n + 1) \cdot \frac{n (n + 1)}{2}

megegyezik a jó háromszögek számának háromszorosával, hiszen minden jó háromszöget mindhárom csúcsánál számoltunk.
Tehát a jó háromszögek száma

\frac{n (n + 1) (2 n + 1)}{6} .

II. megoldás. A

(2 n + 1)

-szög csúcsai összesen

(\binom{2 n + 1}{3})

háromszöget határoznak meg. A jó háromszögek számát megkapjuk, ha ebből levonjuk azon (rossz) háromszögek számát, amelyek nem tartalmazzák a sokszög középpontját. Ezeket a háromszögeket a következőképp számoljuk össze.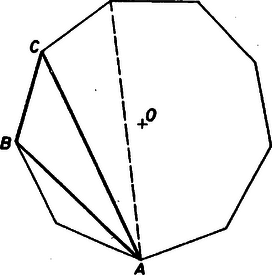

2. ábra

Betűzzük meg a háromszög csúcsait

A

B

C

-vel úgy, hogy

A C

legyen a leghosszabb oldal, és a háromszög körüljárása negatív legyen (ekkor az

A C

egyenes elválasztja

B

-t a sokszög középpontjától, 2. ábra). Minden rossz háromszöghöz egyértelműen tartozik egy betűzés. Ha

A

-t rögzítjük, akkor a sokszög

A

után negatív körüljárási irányban következő

n

csúcsa közül bármelyik kettőt kiválasztva kapunk egy rossz háromszöget, s minden olyan rossz háromszöget megkapunk így, amelynek

A

csúcsa a rögzített csúcs. Ezen háromszögek száma tehát

(\binom{n}{2}) . A -t (2 n + 1)

-féleképpen rögzíthetjük, így a rossz háromszögek száma

(2 n + 1) \cdot (\binom{n}{2})

.
A jó háromszögek száma:

\begin{matrix} (\binom{2 n + 1}{3}) - (2 n + 1) \cdot (\binom{n}{2}) = \frac{2 n + 1}{6} [2 n (2 n - 1) - 3 n (n - 1)] = \frac{2 n + 1}{6} (n^{2} + n) = \frac{n (n + 1) (2 n + 1)}{6} . \end{matrix}

György András (Budapest, Árpád Gimn., II. o. t.) dolgozata alapján