| Feladat: | Gy.2752 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Füzet: | 1992/október, 304 - 305. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Magasabb fokú egyenletek, Függvényegyenletek, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1992/február: Gy.2752 | ||
|
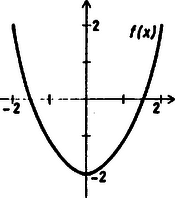
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A bizonyítást többféle módon is végezhetjük. Kiszámolhatjuk -et,majd az így kapott nyolcadfokú egyenletet megoldjuk (könnyen felírhatjuk első és harmadfokú tényezők szorzataként). Az is elegendő, ha mutatunk csatlakozó intervallumokat, ahol a függvény előjelet vált. Most egy egyszerűbb, de legalábbis kevésbé számolós megoldást mutatunk.
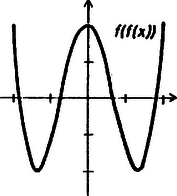
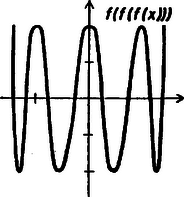
Felrajzolva grafikonját látható, hogy a , illetve a intervallumban felveszi a zárt intervallum minden értékét, méghozzá mindegyiket pontosan egyszer. Ezután ugyanígy a és a is 2‐2 részre osztható, amelyeken veszi fel egyszeresen a ] intervallum számait (az egyes részintervallumok: , , bár a konkrét értékekre nincs is szükségünk), majd ezek mindegyike további két részre osztható, ahol viselkedik ugyanígy. Ez az összesen nyolc intervallum lefedi az egész intervallumot. Felrajzolhatjuk sematikus grafikonját. A nyolc intervallum mindegyikében pontosan egy megoldása van az egyenletnek, és azok, az utolsót kivéve, az intervallumok belsejében találhatók, így nem eshetnek egybe. Tehát kaptunk nyolc különböző valós megoldást, és több megoldás nincs, mivel az egyenlet nyolcadfokú. |