Kezdőlap


Feladat:	Gy.2738	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Baksa Klára , Maróti Attila , Megyesi Zoltán , Németh Olívia , Németh Tamás , Pázmándi Tamás , Révai András , Rózsa Gábor , Sallai Sándor , Scharf Zoltán
Füzet:	1992/november, 379 - 380. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Magasságpont, Síkgeometriai számítások trigonometria nélkül háromszögekben, Pitagorasz-tétel alkalmazásai, Gyakorlat
Hivatkozás(ok):	Feladatok: 1991/december: Gy.2738

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy a magasságpont $B$ -hez van a legközelebb. Ennek bizonyításához az alábbi segédtételt igazoljuk: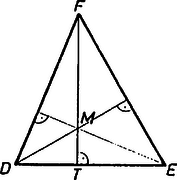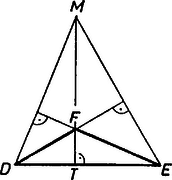
Egy háromszög két csúcsa közül a magasságponthoz az van közelebb, amelyik a harmadik csúcshoz közelebb van.

Jelöljük a háromszög két csúcsát

D

-vel és

E

-vel, a magasságpontot

M

-mel, a háromszög harmadik csúcsát

F

-fel, az

F

-hez tartozó magasság talppontját pedig

T

-vel. Az

F D T

F E T

M D T

és

M E T

háromszögek derékszögűek, ezért Pitagorasz tétele szerint

\begin{matrix} M D^{2} & = M T^{2} + D T^{2} = M T^{2} + F D^{2} - T F^{2} és \\ M E^{2} & = M T^{2} + E T^{2} = M T^{2} + F E^{2} - T F^{2} . \end{matrix}

Tehát

M D^{2} - M E^{2} = F D^{2} - F E^{2}

, vagyis

M D

pontosan akkor nagyobb

M E

-nél, ha

F D

nagyobb

F E

-nél. Ezzel segédtételünket beláttuk.
Eredeti feladatunkban

C A > C B

és

A C > A B

, ezért

M A > M B

és

M C > M B

; tehát

B

-hez van legközelebb a magasságpont.