Kezdőlap


Feladat:	Gy.2723	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csiszár Villő
Füzet:	1992/május, 209 - 210. oldal		PDF \| MathML
Témakör(ök):	Hossz, kerület, Háromszögek hasonlósága, Algebrai átalakítások, Négyzetek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1991/október: Gy.2723

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A keletkező 8 háromszög (4 satírozott és 4 üresen maradt) hasonló, mert mindegyikben van egy-egy derékszög, s a szomszédos háromszögeknek a közös csúcsnál lévő szögei csúcsszögek, tehát egyenlők.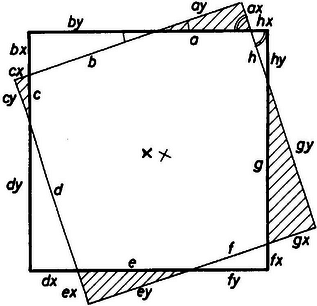

Jelöljük az átfogókat az ábrának megfelelően

a, b, c, d, e, f, g, h

-val. A hasonlóság miatt a 8 háromszögben megegyezik a befogóknak az átfogókhoz való aránya. Legyen ez a két arány

x

és

y

. Ekkor a 8 háromszög befogói rendre

a x

a y

b x

...

h y .

A két egybevágó négyzet kerülete egyenlő:

\begin{matrix} (a y + b + c x) + (c y + d + e x) + (e y + f + g x) + (g y + h + a x) = \\ = (h x + a + b y) + (b x + c + d y) + (d x + e + f y) + (f x + g + h y) . \end{matrix}

Az egyenletet rendezve kapjuk, hogy

\begin{matrix} (x + y - 1) (a + c + e + g) = (x + y - 1) (b + d + f + h) . \end{matrix}

Mivel egy derékszögű háromszögben a két befogó összege nagyobb, mint az átfogó, ezért

x + y > 1,

így a fenti egyenletet megszorozhatjuk

\frac{x + y}{x + y - 1}

-gyel:

\begin{matrix} (x + y) (a + c + e + g) = (x + y) (b + d + f + h), vagyis \\ (a x + a y) + (c x + c y) + (e x + e y) + (g x + g y) = \\ = (b x + b y) + (d x + d y) + (f x + f y) + (h x + h y) . \end{matrix}

Ez viszont éppen a bizonyítandó állítás.

Csiszár Villő (Budapest, Karinthy F. Gimn., II. o. t.)