Kezdőlap


Feladat:	Gy.2708	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Csorba Péter , Csörnyei Marianna , Faragó Gergely , Futó Gábor , Galambos István , Hegedűs Márton , Kerekes Balázs , Megyesi Zoltán , Molnár-Sáska Gábor , Németh Ákos , Szatmári Alexandra
Füzet:	1992/április, 158 - 159. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Terület, felszín, Számtani-mértani egyenlőtlenségek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1991/május: Gy.2708

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Használjuk az ábra jelöléseit.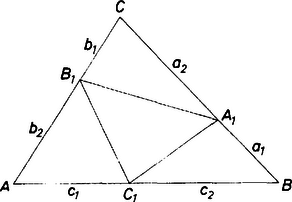
Tudjuk, hogy ha két háromszög egyik szöge közös, akkor a háromszögek területének aránya megegyezik a közös szöget bezáró két-két oldal szorzatának arányával. (Ez következik a $t = \frac{a b \cdot sin γ}{2}$ területképletből, de szögfüggvények használata nélkül is egyszerűen belátható.)

Esetünkben

\begin{matrix} t_{A C_{1} B_{1}} = t_{B A_{1} C_{1}} = t_{C A_{1} B_{1}} = \frac{1}{4} t_{A B C}, \end{matrix}

vagyis:

\begin{matrix} c_{1} b_{2} = \frac{1}{4} (c_{1} + c_{2}) (b_{1} + b_{2}), \\ a_{1} c_{2} = \frac{1}{4} (a_{1} + a_{2}) (c_{1} + c_{2}), \\ b_{1} a_{2} = \frac{1}{4} (b_{1} + b_{2}) (a_{1} + a_{2}) . \end{matrix}

A három egyenletet összeszorozva és rendezve:

\begin{matrix} a_{1} \cdot a_{2} \cdot b_{1} \cdot b_{2} \cdot c_{1} \cdot c_{2} = {(\frac{a_{1} + a_{2}}{2})}^{2} \cdot {(\frac{b_{1} + b_{2}}{2})}^{2} \cdot {(\frac{c_{1} + c_{2}}{2})}^{2} . \end{matrix}

A számtani és mértani közép közti egyenlőtlenség miatt (bármely

x, y

pozitív számokra

x \cdot y \leq {(\frac{x + y}{2})}^{2}

, egyenlőség csak

x = y

esetén) ez az egyenlőség csak akkor állhat fenn, ha

a_{1} = a_{2}

b_{1} = b_{2}

és

c_{1} = c_{2}

. Ez viszont éppen azt jelenti, hogy

A_{1}

B_{1}

és

C_{1}

felezik a háromszög oldalait.

Kerekes Balázs (Miskolc, Földes F. Gimn., II. o. t.) dolgozata alapján