Feladat: Gy.2701 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Csörnyei Marianna ,  Futó Gábor ,  Galambos István ,  Kálmán Tamás ,  Kerekes Balázs ,  Marx Gábor ,  Megyesi Zoltán ,  Molnár-Sáska Gábor ,  Németh Ákos ,  Párniczky Benedek ,  Rákóczi Bálint ,  Róka Dániel ,  Szendrei Tamás ,  Szeredi Tibor ,  Veres Gábor 
Füzet: 1993/január, 17 - 18. oldal  PDF  |  MathML 
Témakör(ök): Párhuzamos szelők tétele, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1991/április: Gy.2701

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a feladatot megoldottnak. Jelöljük a három félegyenest a, b, c-vel, a közös végpontjukat O-val, a három szögtartományban adott pontokat pedig az 1.ábrán látható elhelyezkedés szerint P, Q, R-rel. Húzzunk Q-n és R-en át párhuzamosokat c-vel, messék ezek b-t és a-t K-ban, illetve L-ben, végül QR és KL metszéspontját jelöljük T-ve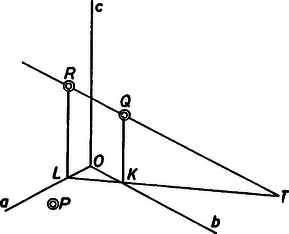l.

 
 

1. ábra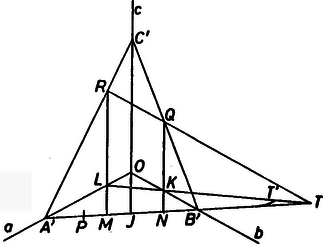
 

 
 

2. ábra
 

Legyen C' olyan pontja a c félegyenesnek, amelyre C'R metszi a-t, C'Q pedig metszi b-t. (Ez teljesül, ha C' ,,elég messze'' van O-tól.) Legyen a két metszéspont A', illetve B' (2. ábra). Megmutatjuk, hogy az A'B' egyenes ‐ C' helyzetétől függetlenül ‐ mindig átmegy T-n. Jelöljük A'B' és LK metszéspontját T'-vel. Bebizonyítjuk, hogy T'≡T. Legyen az RL, C'O és QK egymással párhuzamos egyeneseknek A'B'-vel való metszéspontja rendre M, J és N. Mivel RM∥C'J és C'J∥QN, ezért
RLLM=C'OOJésC'OOJ=QKKN,vagyisRLLM=QKKN.
Átrendezve KNLM=QKRL.
Másrészt KN és LM az LT'M szög, QK és RL pedig az RTL szög párhuzamos szelői, ezért
KNLM=KT'LT'ésQKRL=KTLT,vagyisKT'LT'=KTLT.
Ez utóbbi viszont csak akkor teljesülhet, ha T'≡T. Tehát A'B' mindig átmegy T-n.
Ezek alapján a szerkesztés menete a következő: R és Q ismeretében megszerkesztjük a T pontot. A TP egyenes kimetszi az a és b félegyenesekből az A és B pontokat, végül AR és c közös pontja lesz C. A párhuzamos szelők tételének segítségével könnyen belátható, hogy az így szerkesztett ABC háromszög BC oldala átmegy Q-n, tehát a háromszög eleget tesz a feladat feltételeinek. (Ha az RQ és LK egyenesek párhuzamosak, akkor a szerkesztésben TP szerepét a P-n átmenő, RQ-val párhuzamos egyenes veszi át.)
A feladatnak mindig egy megoldása van, hacsak az adódó A,B pontpárra AO>KO és BO>LO.
 

 Róka Dániel (Budapest, Szt.István Gimn., II. o. t.) dolgozata alapján
 
Megjegyzések 1. A megoldás során nem használtuk ki, hogy a szögtartományok 120∘-osak. Ez a feltétel csak a diszkussziót teszi egyszerűvé.
2. Feladatunk tulajdonképpen a következő egyszerű térgeometriai feladat síkra vetített változata: Adott egy kocka három szomszédos lapján a P, Q és R pont. Szerkesszük meg a három lap közös csúcsából kiinduló három élen az A, B, C pontokat úgy, hogy az ABC háromszög oldalai átmenjenek a P, Q, R pontokon (3. ábra).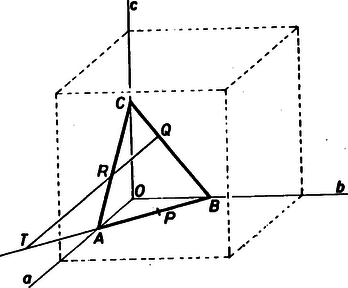
 
 

3. ábra
 

Ennek megoldása egyszerű: a PQR sík kimetszi az élekből az A, B, C pontokat. Viszont ez a megoldás mutatja az eredeti megoldásunkban nagyon fontos T pont szerepét: T nem más, mint az RQ egyenesnek és a kocka P-t tartalmazó lapjának a döféspontja, ezt LK-val, RQ-nak azon a lapon lévő vetületével metszettük ki.