Kezdőlap


Feladat:	Gy.2698	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kálmán Tamás
Füzet:	1992/november, 373 - 374. oldal		PDF \| MathML
Témakör(ök):	Húrsokszögek, Ellenpélda, mint megoldási módszer a matematikában, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1991/április: Gy.2698

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Nem következik. Egyszerűen konstruálhatunk ellenpéldát: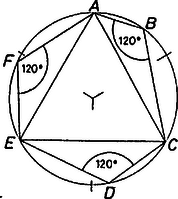

1. ábra

Tekintsük az

A C E

szabályos háromszöget és a körülírt körét. Legyenek a

B

D

F

pontok rendre a kisebbik

A C

C E

E A

íveknek a felezőponttól különböző pontjai (1. ábra). Ekkor az

A E C B

négyszög húrnégyszög, tehát

A B C ∢ = 180^{\circ} - A E C ∢ = 180^{\circ} - 60^{\circ} = 120^{\circ}

. Hasonlóan látható be, hogy

C D E ∢ = E F A ∢ = 120^{\circ}

. Vagyis az

A B C D E F

hatszögnek (legalább) három

120^{\circ}

-os szöge van, de nem szabályos, mert például

A B \neq B C

. (Tulajdonképpen az is elég, ha

B

D

F

közül csak egyik különböző a felezőponttól.)

Megjegyzés: Könnyen látható, hogy ha a (nem egyenlő szárú)

B A C

D C E

F E A

háromszögek egybevágóak és azonos körüljárásúak, akkor hatszögünk valamennyi szöge

120^{\circ}

-os, és az mégsem szabályos.

II. megoldás. A feladatot a következő, általános esetben oldjuk meg: Egy körbe írt

n

-szögnek minden szöge egyenlő. Következik-e ebből, hogy a sokszög szabályos?
Először megmutatjuk, ha

n

páratlan, akkor a válasz igenlő. Tudjuk, hogy egy (konvex)

n

-szög belső szögeinek összege

(n - 2) \cdot 180^{\circ}

, ezért ha minden szög egyenlő, akkor minden szög

\frac{(n - 2) \cdot 180^{\circ}}{n}

. Ha a sokszöget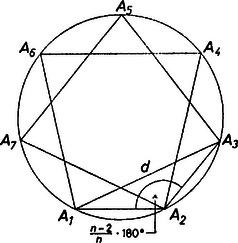

A_{1} A_{2} ... A_{2 k + 1}

jelöli

(n = 2 k + 1)

, akkor

\frac{n - 2}{n} \cdot 180^{\circ} = A_{1} A_{2} A_{3} ∢ = A_{2} A_{3} A_{4} ∢ = ... = A_{2 k + 1} A_{1} A_{2} ∢

2. ábra

A sokszög köré írt körben az

A_{1} A_{3}

A_{2} A_{4}

...

A_{2 k} A_{1}

A_{2 k + 1} A_{2}

húrokhoz ugyanakkora kerületi szög tartozik, vagyis ezek a húrok egyenlő hosszúak; jelöljük ezt a hosszúságot

d

-vel (2. ábra). Ha tehát az

A_{1}

pontból kiindulva egy irányba haladva mindig

d

távolságot mérünk fel a körvonalra, akkor rendre az

A_{3}

A_{5}

...

A_{2 k + 1}

A_{2}

A_{4}

...

A_{2 k}

pontokat kapjuk, vagyis meg tudjuk szerkeszteni a sokszöget. Viszont tudjuk, hogy a szabályos

n

-szögnek is minden szöge

\frac{n - 2}{n} \cdot 180^{\circ}

, ezért a szerkesztés során kapott

A_{1} A_{2} ... A_{2 k + 1}

sokszög csak szabályos lehet. Ezzel beláttuk, hogy ha

n

páratlan, akkor a kérdésre ,,igen'' a válasz.
Ha

n

páros, akkor viszont a válasz nemleges. Az I. megoldásban leírthoz hasonlóan konstruálunk ellenpéldát. Legyen

n = 2 k

, írjunk egy körbe két szabályos

k

-szöget úgy, hogy azok ne legyenek a kör középpontja körül

\frac{2 π}{n} = \frac{π}{k}

nagyságú szöggel egymásba forgathatók. Ez azt jelenti, hogy az egyik

k

-szög bármely

P Q

oldalához tartozó kisebbik ív felezőpontja nem csúcsa a másik

k

-szögnek. Ezen az íven a másik

k

-szögnek nyilván pontosan egy

R

csúcsa van, amire az előbbiek szerint

P R \neq R Q

, viszo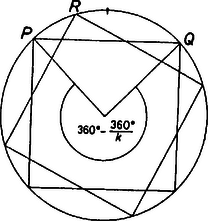nt

P R Q ∢ = \frac{1}{2} (360^{\circ} - \frac{360^{\circ}}{k}) = 180 \cdot \frac{n - 2}{n}

(3.ábra).

3. ábra

A két

k

-szög csúcsainak konvex burkaként kapott

n

-szögnek tehát minden szöge egyenlő, de oldalai között vannak különbözőek.

Kálmán Tamás (Fazekas M. Főv. Gyak. Gimn., II. o. t.)