Kezdőlap


Feladat:	Gy.2687	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1991/november, 394. oldal		PDF \| MathML
Témakör(ök):	Algebrai átalakítások, Paraméteres egyenlőtlenségek, Terület, felszín, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1991/március: Gy.2687

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az

\begin{matrix} f (x) = x^{2} - x (a + b + c) + a b + b c + c a \end{matrix}

jelöléssel azt kell igazolnunk, hogy

f (d) ≧ 0

. Könnyen látható, hogy

\begin{matrix} x \cdot f (x) - a b c = (x - a) (x - b) (x - c), \end{matrix}

tehát

\begin{matrix} f (d) = \frac{(d - a) (d - b) (d - c) + a b c}{d}, \end{matrix}

(1)

ahonnan a bizonyítandónál élesebb

\begin{matrix} f (d) ≧ \frac{a b c}{d} \end{matrix}

egyenlőtlenséget kapjuk, hiszen (1) számlálójában

(d - a) (d - b) (d - c) ≧ 0

II. megoldás. Az alábbi megoldás geometriai jelentést tulajdonít a feladatban szereplő mennyiségeknek. Tekintsünk egy

d

oldalú

A B C

szabályos háromszöget, melynek csúcsaiból az ábra szerint azonos körüljárás szerint mérjük fel az

a

b

illetve a

c

hosszúságú szakaszokat.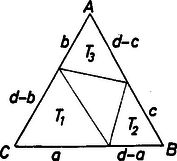

A

B

és

C

csúcsú kis háromszögek területének összege nyilván kisebb, mint az

A B C

háromszögé. A területeket a

60^{\circ}

-os szög felhasználásával felírva

\begin{matrix} T_{1} = \frac{\sqrt[]{3}}{4} \cdot a (d - b); T_{2} = \frac{\sqrt[]{3}}{4} c (d - a); \end{matrix}

\begin{matrix} T_{3} = \frac{\sqrt[]{3}}{4} b (d - c); T_{A B C} = \frac{\sqrt[]{3}}{4} \cdot d^{2} . \end{matrix}

T_{1} + T_{2} + T_{3} < T

egyenlőtlenség mindkét oldalát

\frac{\sqrt[]{3}}{4}

-gyel osztva a bizonyítandó egyenlőtlenséget kapjuk.

Megjegyzés. Mindkét bizonyításból kiderül, hogy a feltételek mellett a bizonyítandó egyenlőtlenségben nem állhat egyenlőség.