Kezdőlap


Feladat:	Gy.2685	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1992/november, 370 - 372. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Kocka, Sík egyenlete, Koordináta-geometria, Térelemek és részeik, Térgeometriai számítások trigonometria nélkül, Gyakorlat
Hivatkozás(ok):	Feladatok: 1991/február: Gy.2685

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Három esetet különböztetünk meg attól függően, hogy $X$ az $A B$ él belső pontja, vagy pedig a szakasz $A$ -n, vagy $B$ -n túli meghosszabbításán helyezkedik el. A részletes számításokat abban az esetben végezzük el, ha $X$ az $A B$ él belső pontja.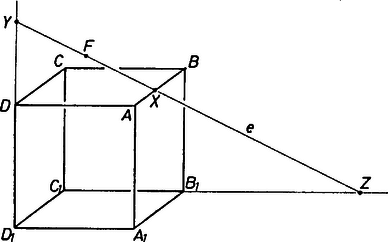

1. ábra

Jelöljük

F

-fel az

X Y

szakasz felezőpontját.

X

, illetve

Y

az egymással párhuzamos

A B A_{1} B_{1}

, illetve

C D C_{1} D_{1}

sík egy-egy pontja, ezért

F

rajta van e két sík középpárhuzamos síkján; tehát

F

távolsága e két lapsíktól

\frac{1}{2}

. Vetítsük a kockát és az

e

egyenest az

A B A_{1} B_{1}

oldallap síkjára.

F

és

Y

vetülete legyen

F'

és

Y'

, az

F'

-ből az

A A_{1} B B_{1}

négyzet oldalaira bocsátott merőlegesek talppontjai pedig a 2. ábra szerint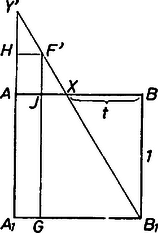

G, H

és

J

2. ábra

A merőleges vetítés megőrzi a képsíkkal párhuzamos szakaszok hosszát és az egy egyenesre illeszkedő szakaszok arányát; ezért

F' G

megegyezik

F

-nek az

A_{1} B_{1} C_{1} D_{1}

laptól való távolságával,

F' H

pedig

F

-nek az

A D A_{1} D_{1}

laptól való távolságával, továbbá

F'

Y' X

szakasz felezőpontja. Az

Y' A X

és a

B_{1} B X

derékszögű háromszögek hasonlósága folytán

\begin{matrix} \frac{Y' A}{A X} = \frac{B_{1} B}{B X}, vagyis Y' A = \frac{A X \cdot B_{1} B}{B X} = \frac{(1 - t) \cdot 1}{t} = \frac{1 - t}{t} . \end{matrix}

Ezért

\begin{matrix} F' J = \frac{1}{2} Y' A = \frac{1 - t}{2 t}, F' G = F' J + J G = \frac{1 - t}{2 t} + 1 = \frac{1 + t}{2 t}, \\ F' H = \frac{1}{2} A X = \frac{1 - t}{2}, \end{matrix}

végül pedig

F

-nek a

B C B_{1} C_{1}

laptól való távolsága

1 - F' H = \frac{1 + t}{2}

.
Lényegében ugyanígy határozhatjuk meg a távolságokat akkor is, ha

X

A B

szakasz valamelyik meghosszabbításán van. Az eredményeket a következő táblázatban foglaljuk össze:

\begin{matrix} Ftávolsága a laptól, haXazA Bszakasz \\ a lap & belső pontja & A-n túli & B-n túli \\ meghosszabbításán van & meghosszabbításán van \\ A B C D & \frac{1 - t}{2 t} & \frac{t - 1}{2 t} & \frac{1 + t}{2 t} \\ A_{1} B_{1} C_{1} D_{1} & \frac{1 + t}{2 t} & \frac{1 + t}{2 t} & | \frac{1 - t}{2 t} | \\ A B A_{1} B_{1} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ C D C_{1} D_{1} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ A D A_{1} D_{1} & \frac{1 - t}{2} & \frac{t - 1}{2} & \frac{1 + t}{2} \\ B C B_{1} C_{1} & \frac{1 + t}{2} & \frac{1 + t}{2} & | \frac{1 - t}{2} | \end{matrix}

II. megoldás. Helyezzük el a kockát egy térbeli derékszögű koordináta rendszerben úgy, hogy

C_{1}

legyen az origó,

D_{1}, B_{1}

és

C

pedig rendre az

x, y, z

tengely pozitív felére illeszkedjen. Ekkor

A

koordinátái

(1; 1; 1)

B

koordinátái

(0; 1; 1)

, hasonlóan

C (0; 0; 1)

D (1; 0; 1)

A_{1} (1; 1; 0)

B_{1} (0; 1; 0)

C_{1} (0; 0; 0)

D_{1}

pedig

(1; 0; 0)

. Az

A B

egyenes az

y = 1

egyenletű

A B A_{1} B_{1}

és a

z = 1

egyenletű

A B C D

síkok metszésvonala, tehát az erre az egyenesre illeszkedő

X

pont második és harmadik koordinátája is

1

. Legyen

X

első koordinátája

t

; ekkor

B X = | t |

(3. ábra).

3. ábra

e

egyenes metszi a

B_{1} C_{1}

egyenest, tehát benne van a

B_{1} C_{1} X

síkban. A

B_{1}

C_{1}

és

X

pontok koordinátái kielégítik az

x = t z

egyenletet, tehát ez a

B_{1} C_{1} X

sík egyenlete. Az

Y

pont rajta van a

B_{1} C_{1} X

, az

A D A_{1} D_{1}

és a

C D C_{1} D_{1}

síkokon. E két utóbbi egyenlete,

x = 1

és

y = 0

. Tehát

Y

koordinátái kielégítik az

x = 1

y = 0

és

y = t z

egyenleteket, azaz

Y (1; 0; \frac{1}{t})

. Így

X Y

felezőpontjának koordinátái:

\begin{matrix} F (\frac{1}{2} (t + 1); \frac{1}{2} (1 + 0); \frac{1}{2} (1 + \frac{1}{t})) . \end{matrix}

A kocka oldallapjainak egyenletei és

F

-nek ezen oldallapoktól való távolsága:

\begin{matrix} \begin{matrix} A B C D : & z = 1 | \frac{1 + t}{2 t} - 1 | = | \frac{1 - t}{2 t} |; \\ A_{1} B_{1} C_{1} D_{1} : & z = 0 | \frac{1 + t}{2 t} |; \\ A B A_{1} B_{1} : & y = 1 | \frac{1}{2} - 1 | = \frac{1}{2}; \\ C D C_{1} D_{1} : & y = 0 | \frac{1}{2} - 0 | = \frac{1}{2}; \\ A D A_{1} D_{1} : & x = 1 | \frac{1 + t}{2} - 1 | = | \frac{t - 1}{2} |; \\ B C B_{1} C_{1} : & x = 0 | \frac{1 + t}{2} | . \end{matrix} \end{matrix}

(Ezekből a képletekből egyszerű számolással kaphatjuk az I. megoldás végén található táblázatot, ha felhasználjuk, hogy

B X = | t |