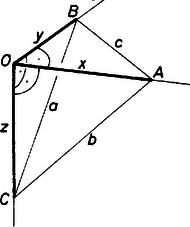
Tegyük fel, hogy egy kocka $O$ csúcsából kiinduló három éle közül egy-egy átmegy az adott pontokon, amelyeket $A\mathrm{,}B\mathrm{,}C$-vel jelölünk. (A feladat szövegéből következik, hogy a kocka csúcsából kiinduló három él sorra átmegy egy-egy adott ponton.) Jelöljük az $ABC$ háromszög oldalait a szokásos módon $a\mathrm{,}b\mathrm{,}c$-vel (ha $A\mathrm{,}B$ és $C$ egy egyenesbe esik, akkor nyilván nem létezik megfelelő kocka), az $OA\mathrm{,}OB\mathrm{,}OC$ távolságokat pedig rendre $x\mathrm{,}y\mathrm{,}z$-vel.