Feladat: Gy.2675 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Futó Gábor ,  Molnár-Sáska Gábor 
Füzet: 1992/január, 19 - 20. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Párhuzamos szelők tétele, Metsző körök hajlásszöge, Gyakorlat
Hivatkozás(ok):Feladatok: 1991/január: Gy.2675

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a feladatot megoldottnak. Jelöljük az adott kört k-val, középpontját O-val, a szerkesztendő kört l-lel, a két adott pontot A-val és B-vel, k és l metszéspontjait P-vel és Q-val, az OA egyenes és l A-tól különböző metszéspontját pedig A'-vel.

 
 

1. ábra
 

Mivel k és l merőlegesen metszik egymást, ezért az OP egyenes érinti l-et. Az OPA' szög tehát az l kör PA' ívéhez tartozó érintőszárú kerületi szög, így megegyezik az ugyanehhez az ívhez tartozó OAP kerületi szöggel. Az OPA' és az OAP háromszögek hasonlóak, hiszen a POA szög közös, egy-egy további szögük pedig egyenlő. Ezért megfelelő oldalaik aránya megegyezik:
OPOA=OA'OP.(1)

 
 

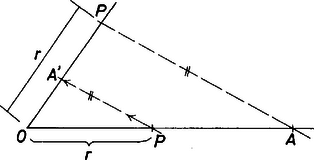2. ábra
 

Ezt felhasználva az OA' szakaszt a ,,negyedik arányos'' ismert szerkesztésével kaphatjuk (2. ábra).
A szerkesztés menete: Az OA és OP ismeretében megszerkesztjük OA'-t. Az OA félegyenesre O-ból felmérjük OA'-t, így kapjuk az A' pontot. Végül az A,B,A' pontokra illeszkedő kört szerkesztjük meg.
Az így szerkesztett l kör esetén az (1) összefüggés teljesül, tehát az OPA' és az OAP háromszögek hasonlóak ‐ megegyezik két-két oldaluk aránya és az azok által bezárt szög ‐, tehát OPA'∢=OPA∢, amiből következik, hogy OP érinti l-et, vagyis l és k merőlegesen metszi egymást.
A feladatnak egy megoldása van, ha O, A és B nem kollineárisak. Ha O, A és B kollineárisak és A' különbözik B-től, akkor nincs megoldás; ha pedig A' egybeesik B-vel, akkor az A-n és A'-n átmenő bármely kör megfelelő.
 

 Molnár-Sáska Gábor (Budapest, Fazekas M. Gyak. Gimn., II. o. t.) dolgozata alapján
 

Megjegyzés. Az A' ponthoz hasonlóan szerkeszthetjük meg azt a B' pontot, amelyre OPOB=OB'OP. Ezekre a pontokra OP2=OA⋅OA'=OB⋅OB'. (Ezt az értéket az O pont l-re vonatkozó hatványának nevezzük.) Könnyen belátható, hogy az A,B,A',B' pontok egy körön vannak, azaz természetesen ugyanazt a kört kapjuk, ha az A,A' pontpár helyett a B,B' párt használjuk a szerkesztés során.