Kezdőlap


Feladat:	Gy.2669	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csikai Szabolcs
Füzet:	1991/október, 315 - 316. oldal		PDF \| MathML
Témakör(ök):	Egyenes körkúpok, Terület, felszín, Térfogat, Pitagorasz-tétel alkalmazásai, Gyakorlat
Hivatkozás(ok):	Feladatok: 1990/december: Gy.2669

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög oldalait és magasságait a szokásos módon $a$ , $b$ , $c$ , $m_{a}$ , $m_{b}$ , $m_{c}$ -vel. Ha a háromszöget egyik oldalegyenese körül megforgatjuk, akkor a keletkező test vagy egy körkúp, vagy két körkúp összege vagy különbsége, attól függően, hogy a háromszögnek a forgástengelyre illeszkedő szögei között nincs tompaszög, illetve van. A keletkező test térfogata az egyes esetekben (az ábra jelöléseit használva):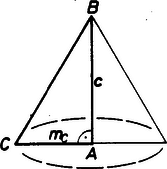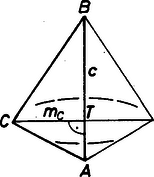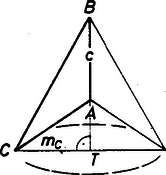

\begin{matrix} V_{1} = \frac{π}{3} \cdot A C^{2} \cdot A B = \frac{π}{3} \cdot m_{c}^{2} \cdot c, \\ V_{2} = \frac{π}{3} \cdot C T^{2} \cdot A T + \frac{π}{3} \cdot C T^{2} \cdot B T = \frac{π}{3} \cdot m_{c}^{2} \cdot c, \\ V_{3} = \frac{π}{3} \cdot C T^{2} \cdot B T - \frac{π}{3} \cdot C T^{2} \cdot A T = \frac{π}{3} \cdot m_{c}^{2} \cdot c . \end{matrix}

Tehát ha a háromszöget a

c

oldal egyenese körül forgatjuk, akkor a keletkező test térfogata minden esetben

\frac{π}{3} \cdot m_{c}^{2} \cdot c

. Ugyanúgy

V_{a} = \frac{π}{3} \cdot m_{a}^{2} \cdot a

és

V_{b} = \frac{π}{3} \cdot m_{b}^{2} \cdot b

. Ezeket eredeti egyenlőségünkbe helyettesítve, majd rendezve kapjuk, hogy:

\begin{matrix} \frac{1}{m_{a}^{4} \cdot a^{2}} = \frac{1}{m_{b}^{4} \cdot b^{2}} + \frac{1}{m_{c}^{4} \cdot c^{2}} . \end{matrix}

(1)

Ha a háromszög területe

t

, akkor

16 t^{4} = m_{a}^{4} \cdot a^{4} = m_{b}^{4} \cdot b^{4} = m_{c}^{4} \cdot c^{4}

. Ezt felhasználva (1)-et így írhatjuk:

\begin{matrix} \frac{1}{\frac{t^{4}}{a^{2}}} = \frac{1}{\frac{t^{4}}{b^{2}}} + \frac{1}{\frac{t^{4}}{c^{2}}}, \end{matrix}

vagyis:

\begin{matrix} a^{2} = b^{2} + c^{2} . \end{matrix}

Ebből Pitagorasz tételének megfordítása alapján következik, hogy az

a

oldallal szemközti szög derékszög; tehát a háromszög legnagyobb szöge

90^{\circ}

-os.