Kezdőlap


Feladat:	Gy.2660	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1991/december, 456 - 457. oldal		PDF \| MathML
Témakör(ök):	Gyökös függvények, Derékszögű háromszögek geometriája, Terület, felszín, Számtani-mértani egyenlőtlenségek, Szélsőérték-feladatok differenciálszámítás nélkül, Gyakorlat
Hivatkozás(ok):	Feladatok: 1990/november: Gy.2660

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $O$ az $A B$ átmérőjű kör középpontja, $T$ a $P$ pont $A B$ egyenesen lévő merőleges vetülete, $R$ pedig a $P$ -t tartalmazó $A B$ ív felezőpontja.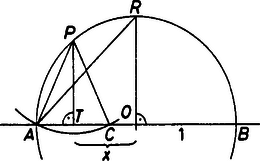

A feladatban megadott feltételek alapján

P A = P C

, tehát az

A P C

háromszög egyenlő szárú, azaz

A T = T C

; így a háromszög területe:

\begin{matrix} T_{A P C} = A T \cdot T P . \end{matrix}

(1)

Ennek a kifejezésnek kell a maximumhelyét ill. helyeit meghatároznunk.
Tekintsük először azt az esetet, amikor

T

A O

szakasz belső pontja. Ekkor (1) értéke nem lehet maximális, hiszen

A T < A O

és

T P < O R

miatt

\begin{matrix} T_{A P C} = A T \cdot T P < A O \cdot O R = T_{A R B} . \end{matrix}

A következőkben a másik esetet vizsgáljuk, ha

T

B O

szakasz

B

-től különböző pontja.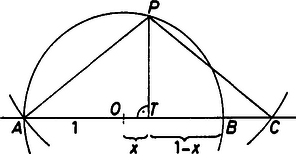

A kör sugarát egységnyinek választjuk. Jelöljük az

O T

szakasz hosszát

x

-szel, amire ekkor

0 ≦ x < O A = 1

teljesül.
Írjuk fel az

A P B

derékszögű háromszögre a magasságtételt:

\begin{matrix} T P = \sqrt[]{A T \cdot T B} = \sqrt[]{(1 + x) (1 - x)} . \end{matrix}

Ezt az (1) egyenletbe helyettesítve kapjuk, hogy

\begin{matrix} T_{A P C} = A T \cdot T P = (1 + x) \sqrt[]{(1 + x) (1 - x)} = \sqrt[]{{(1 + x)}^{3} (1 - x)} . \end{matrix}

(2)

Mivel az

y \mapsto c \sqrt[]{y}

függvény (ahol

c > 0

, állandó,

y > 0

) szigorúan növő, ezért a fenti kifejezés pontosan akkor a legnagyobb, amikor a

\sqrt[4]{{(1 + x)}^{3} (1 - x) \cdot 3}

az.
Alkalmazzuk a számtani és mértani közép közötti egyenlőtlenséget:

\begin{matrix} \sqrt[4]{{(1 + x)}^{3} (3 - 3 x)} ≦ \frac{(1 + x) + (1 + x) + (1 + x) + (3 - 3 x)}{4} = \frac{3}{2} . \end{matrix}

Innen látható, hogy a bal oldali kifejezés pontosan akkor maximális, amikor a tényezői egyenlőek, vagyis

1 + x = 3 - 3 x

x = \frac{1}{2}

esetén.
Tehát az

A P C

háromszög területe akkor a legnagyobb, ha

T

O B

szakasz felezőpontja.