Feladat: Gy.2659 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Hegedűs Andrea ,  Kovács Szabolcs ,  Marx Gábor 
Füzet: 1991/október, 312 - 313. oldal  PDF  |  MathML 
Témakör(ök): Szögfelező egyenes, Beírt kör, Húrnégyszögek, Síkgeometriai bizonyítások, Gyakorlat
Hivatkozás(ok):Feladatok: 1990/november: Gy.2659

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a beírt kör középpontját O-val, a B-ből a szögfelezőre bocsátott merőleges talppontját T-vel, az ABC háromszög szögeit pedig 2α, 2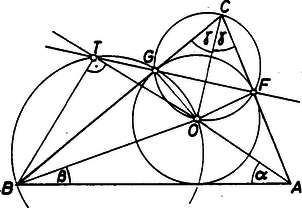β, 2γ-val.

 
 

1. ábra
 

Mivel F és G érintési pontok, ezért OF⊥AC és OG⊥BC. Az OFCG négyszög húrnégyszög, hiszen az F-nél és G-nél lévő szögei derékszögek. Az OTGB négyszög is húrnégyszög, mert az OB szakasz G-ből is és T-ből is derékszögben látszik. Mivel O a beírt kör középpontja, ezért az OA, OB, OC egyenesek szögfelezők, vagyis FCO∢=γ, OAB∢=α, OBA∢=β, így OBT∢=90∘-BOT∢=90∘-(OAB∢+OBA∢)=90∘-(α+β)=γ.
Ezek után a bizonyítást a lehetséges esetek szerint három részre bontjuk:
 

(i) AB>AC. Ekkor T az ABC háromszögön kívül van (1. ábra). Az OBTG húrnégyszögben B és G szemközti csúcsok, ezért OGT∢=180∘-OBT∢=180∘-γ, az OFCG húrnégyszögben pedig OGF∢=OCF∢=γ.
Tehát OGT∢+OGF∢=180∘, vagyis a T, G, F pontok egy egyenesen vannak.
 

(ii) AB=AC. Ekkor T és G egybeesnek, állításunk nyilvánvaló.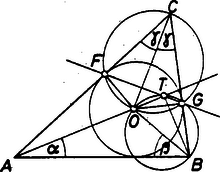
 
 

2. ábra
 

(iii) AB<AC. Ekkor T az ABC háromszög belsejében van (2. ábra). Az OTGB húrnégyszögben OGT∢=OBT∢=γ, az OFCG húrnégyszögben pedig OGF∢=OCF∢=γ. Tehát OGT∢=OGF∢, ezért a G, T, F pontok most is egy egyenesen vannak.
 
 Hegedűs Andrea (Bp., Fazekas M. Gyak.Gimn., II. o. t.) dolgozata alapján