Kezdőlap


Feladat:	Gy.2653	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Horváth István
Füzet:	1991/november, 388 - 389. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Beírt kör, Magasságpont, Körök, Síkgeometriai számítások trigonometria nélkül, Síkgeometriai bizonyítások, Középponti és kerületi szögek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1990/október: Gy.2653

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög szögeit a szokásos módon $α$ , $β$ , $γ$ -val. Az $O$ pont a szögfelezők metszéspontja, ezért

\begin{matrix} A O B ∢ = 180^{\circ} - (\frac{α}{2} + \frac{β}{2}) = 90^{\circ} + \frac{γ}{2} . \end{matrix}

A K B ∢

a körülírt körben az

A B

húrhoz tartozó középponti szög, ezért kétszerese az ugyanehhez a húrhoz tartozó kerületi szögnek:

A K B ∢ = 2 γ

. Az

A M B

szög meghatározásánál három esetet kell megkülönböztetnünk: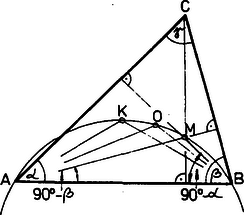

α < 90^{\circ}

és

β < 90^{\circ}

. Ekkor

A M B ∢ = 180^{\circ} - ((90^{\circ} - α) + (90^{\circ} - β) = 180^{\circ} - γ

(1. ábra).

1. ábra

α = 90^{\circ}

vagy

β = 90^{\circ}

. Ekkor a háromszög derékszögű,

M

egybeesik az

A

vagy a

B

csúccs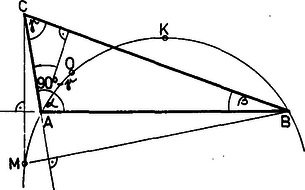al.

α

és

β

egyike tompaszög. Ekkor

A M B ∢ = 180^{\circ} - ((90^{\circ} - γ) + 90^{\circ}) = γ

(2.ábra).

2. ábra

Állításunk bizonyítását is három esetre kell bontanunk a fentieknek megfelelően.
Az 1. esetben az

O

és az

M

pontok az

A B

egyenesnek ugyanazon az oldalán ‐ a háromszög

C

csúcsát tartalmazó oldalán ‐ helyezkednek el, ezért

\begin{matrix} 90^{\circ} + \frac{γ}{2} = A O B ∢ = A M B ∢ = 180^{\circ} - γ, \end{matrix}

vagyis

γ = 60^{\circ}

. Így

A K B ∢ = 120^{\circ}

, tehát

A K B ∢ = A O B ∢

, és

K

is az

A B

egyenesnek

O

-val megegyező oldalán helyezkedik el ‐ az

A B C

háromszög hegyesszögű ‐ vagyis

K

rajta van az

A B O M

körön.
A 2. esetben az

A

B

O

M

pontok mindig egy körön vannak, a

K

pont pedig csak akkor van rajta ezen a körön, ha

90^{\circ} + \frac{γ}{2} = A O B ∢ = A K B ∢ = 2 γ

, vagyis ha

γ = 60^{\circ}

. Állításunk tehát ebben az esetben is igaz, és a háromszög szögei

90^{\circ}

60^{\circ}

30^{\circ}

.
A 3. esetben az

O

és az

M

pontok az

A B

egyenesnek két különböző oldalán helyezkednek el, ezért

A O B ∢ + A M B ∢ = 90^{\circ} + \frac{γ}{2} + γ = 180^{\circ}

, vagyis

γ = 60^{\circ}

. Ebben az esetben

K

A B

egyenesnek

O

-val megegyező oldalán van és

A K B ∢ = 120^{\circ} = A O B^{\circ}

, ezért

K

valóban rajta van az

A B O M

körön.

Horváth István (Fonyód, Magyar B. Ált. Isk. 8. o. t.) dolgozata alapján