Kezdőlap


Feladat:	Gy.2651	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Faragó Gergely , Kálmán Tamás , Veres Gábor
Füzet:	1991/november, 387 - 388. oldal		PDF \| MathML
Témakör(ök):	Körök, Síkgeometriai számítások trigonometria nélkül körökben, Középponti és kerületi szögek, Síkgeometriai bizonyítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1990/október: Gy.2651

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög szögeit $α$ , $β$ , $γ$ -val, a $C A$ oldalt $A$ -ban érintő és $B$ -n átmenő kört $k_{A}$ -val, a másik két kört $k_{B}$ -vel és $k_{C}$ -vel, a $k_{A}$ és $k_{B}$ körök $B$ -től különböző metszéspontját $P$ -vel. Megmutatjuk, hogy a $k_{C}$ kör is átmegy 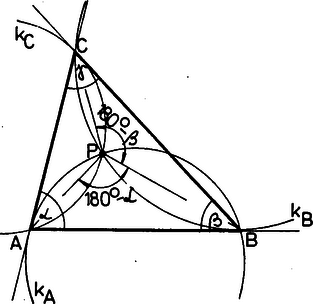$P$ -n.

C A

egyenes érinti a

B

ponton átmenő

k_{A}

kört, ezért a kör a

C A

egyenes által meghatározott két félsík közül abban helyezkedik el, amelyikben a

B

pont. Hasonlóan a

k_{B}

kör az

A B

egyenes által meghatározott két félsík közül a

C

pontot tartalmazóban van. Tehát a

P

pont mindig

C A B

szögtartományban van, sőt mindig az

A B C

háromszög belsejében, mert a

k_{A}

körnek a

C A B

szögtartományba eső íve a

k_{B}

kör két

B C

íve közül azt metszi, amelyik a

B C

egyenesnek

A

-val megegyező oldalán van.
A

k_{A}

körben a

P

-t nem tartalmazó

A B

ívhez tartozó érintőszárú kerületi szög éppen

C A B ∢ = α

. Ezért a

P

-t tartalmazó

A B

ívhez tartozó kerületi szög

180^{\circ} - α

, vagyis

A P B ∢ = 180^{\circ} - α

. Ugyanígy kapjuk, hogy

B P C ∢ = 180^{\circ} - β

. Ezek ismeretében a

C P A

szöget könnyen kiszámolhatjuk:

\begin{matrix} C P A ∢ = 360^{\circ} - (A P B ∢ + B P C ∢) = α + β = 180^{\circ} - γ . \end{matrix}

Ez viszont éppen a

k_{C}

kör egyik

C A

ívéhez tartozó kerületi szög, mert a másik

C A

ívhez tartozó érintőszárú kerületi szög

B C A ∢ = γ

. Tehát az egyik

C A

ív átmegy a

P

ponton.