Feladat: Gy.2644 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1991/április, 162 - 165. oldal  PDF  |  MathML 
Témakör(ök): Gyökös függvények, Derékszögű háromszögek geometriája, Szélsőérték-feladatok differenciálszámítás nélkül, Gyakorlat
Hivatkozás(ok):Feladatok: 1990/szeptember: Gy.2644

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. Válasszuk a négyzet oldalát 2 egységnyinek és legyen F az AB oldal felezőpontja, P és F távolságát pedig jelöljük x-szel. Elegendő azt az esetet vizsgálnunk, amikor PC≧PD, vagyis amikor P az F-től induló, A-t tartalmazó félegyenesen mozog, mert ha P' az F-től induló, B -t tartalmazó félegyenes tetszőleges pontja, akkor P' F-re vonatkozó P tükörképe az A-t tartalmazó félegyenesen mozog, és a szimmetria miatt a B-t tartalmazó félegyenesre vonatkozó korlátok éppen az A-t tartalmazó félegyenesre vonatkozó korlátok reciprokai.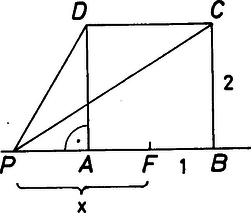
 
 

1. ábra
 

A PBC és a PAD háromszögek derékszögűek, BC=AD=2,PB=1+x és PA=1-x vagy x-1, attól függően, hogy P az FA szakaszon van, vagy nem. Pitagorasz tétele szerint PC=PB2+BC2=(1+x)2+4 és PD=PA2+AD2=(1-x)2+4. Ezekkel
PCPD=(1+x)2+4(1-x)2+4=1+4xx2-2x+5.

A vizsgált arány értéke tehát csak a 4x/(x2-x+5) tört értékétől függ. Mivel x≧0 és a tört nevezője pozitív, ezért a tört minimális értéke 0. Ha a maximális értéket m-mel jelöljük, akkor m az a legnagyobb szám, amelyre a
4xx2-2x+5=m
egyenletnek van valós megoldása, az mx2-(2m+4)x+5m=0 másodfokú egyenlet diszkriminánsa, D=(2m+4)2-20m2 nem negatív. A D≧0 egyenlőtlenséget megoldva kapjuk, hogy
1-52≦m≦1+52.

Tehát a 4x/(x2-2x+5) tört maximális értéke (1+5)/2, így a PC/PD arány legnagyobb értéke
1+1+52=1+52.

Ezt az értéket a szóban forgó arány föl is veszi, mégpedig akkor, ha PF=x=5. Ezért ha a P pont az A-t tartalmazó félegyenesen mozog, akkor
1≦PCPD≦5+12;

ha pedig P a B-t tartalmazó félegyenesen mozog, akkor
1≧PCPD≧1/(5+12)=5-12.

Összefoglalva:
5-12≦PCPD≦5+12.

 
Megjegyzések.
1) Áttekinthetőbbé válik a feladat megoldása, ha felismerjük egy, a geometriai szélsőértékfeladatok megoldása során általában is gyakran használható elv érvényesülését.
Tegyük fel, hogy egy a sík pontjain értelmezett f(P) függvény ‐ jelen esetben a PC/PD arány ‐ szélsőértékeit keressük egy adott Γ görbén: ez most a négyzet AB oldalegyenese. Tekintsük ehhez az F(P)=állandó egyenletű görbesereg elemeit az F függvény úgynevezett nívóhalmazait. Ismeretes, hogy most ezek a görbék körök ‐ a C, D pontokhoz tartozó ún. Apollóniusz-féle körök ‐ illetve PC/PD=1 esetben a CD felező merőlegese.
Egy-egy ilyen vonal két részre osztja a síkot. Az egyik a körvonal belseje, a másik pedig annak külseje. (A felező merőleges esetén persze két félsíkot kapunk.) A két tartomány egyikében az F(P) értéke kisebb, másikban pedig nagyobb, mint a határoló görbén.
Így az F(P) mennyiség a Γ görbén azokban a pontokban veszi föl a szélsőértékét, ahol ennek a körseregnek ‐ az Apollóniusz-féle köröknek ‐ a megfelelő eleme Γ-t, itt az AB egyenest érinti.
Az érintési pont megszerkesztéséhez pedig azt kell tudnunk, hogy a CD szakasz felező merőlegese ‐ a h egyenes ‐ azon pontok mértani helye, ahonnan a fenti körhalmazok minden egyes kör eleméhez egyenlő hosszúságú érintők húzhatók: a h a körsor ún. hatványvonala. Mivel C és D is a körsor elemei ‐ az ún. pontkörök ‐ az F pontból FC=FD hosszúságú érintő húzható minden egyes Apollóniusz-féle körhöz (2. ábra).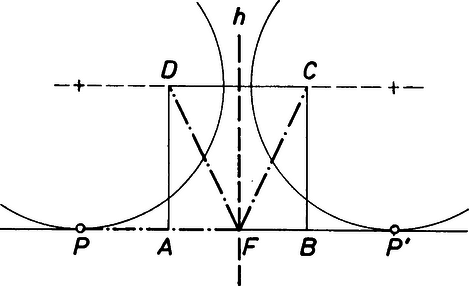
 
 

2. ábra
 

Az AB egyenest érintő körelemek érintési pontjait tehát az F-re szimmetrikusan FP=FC távolságra kapjuk az AB egyenesen. Könnyű számolással kapjuk, hogy ezekre a pontokra az F(P)=PC/PD arány 5+12, illetve ennek reciproka. Az AB egyenes minden további pontja e köröknek külső pontja, így annak tetszőleges Q pontjára
5-12≦QC/QD≦5+12.

2) Sok megoldó csak azt az esetet vizsgálta, amikor P az AB szakaszon mozog. Ekkor a feladat megoldása némileg egyszerűbb, s a kapott korlátok a helyes eredménytől különböznek, hiszen a PC/PD arány x=5 esetén veszi fel a maximumát, tehát amikor P az AB szakaszon kívül van; ezért ezek a dolgozatok csak 2‐3 pontot érdemeltek.