Kezdőlap


Feladat:	Gy.2634	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Reményi Polett , Ujváry-Menyhárt Zoltán
Füzet:	1991/január, 20 - 21. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Középpontos tükrözés, Középvonal, Körülírt kör, Magasságpont, Húrnégyszögek, Síkgeometriai bizonyítások, Háromszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1990/május: Gy.2634

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a $C M$ és $A B$ egyenesek metszéspontját $T$ -vel, $M$ -nek az $A B$ oldalra vonatkozó tükörképét $M^{'}$ -vel, az $A B C$ háromszög szögeit pedig a szokásos módon $α$ , $β$ , $γ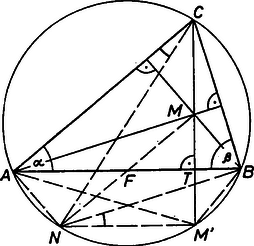$ -val.

Először megmutatjuk, hogy az

N

és

M^{'}

pontok rajta vannak az

A B C

háromszög köré írt körön. Az

A M B

háromszög

F

pontra vonatkozó tükörképe a

B N A

, az

A B

egyenesre vonatkozó tükörképe pedig az

A M' B

háromszög. Ezért

A N B ∢ = A M' B ∢ = A M B ∢ = A M T ∢ + B M T ∢ = 90^{\circ} - M A T ∢ + 90^{\circ} - M B T ∢ = β + α = 180^{\circ} - γ

. Ez azt jelenti, hogy az

A N B C

és az

A M' B C

négyszögek húrnégyszögek, tehát az

A

B

C

N

M'

pontok valóban egy körön vannak.

M N M'

háromszögben

F T

középvonal, ezért

N M'

párhuzamos

F T

-vel, vagyis merőleges

C M

-re, így

C M' N ∢ = 90^{\circ}

. Tehát ‐ Thalesz tételének megfordítása miatt ‐

C N

a körülírt kör egy átmérője, következésképpen

B A N ∢ = C A N ∢ - C A B ∢ = 90^{\circ} - α

. De a

B C N

és a

B A N

szögek ugyanahhoz az ívhez tartoznak, ezért egyenlőek, azaz

B C N ∢ = 90^{\circ} - α

. Az

A C T

derékszögű háromszögben pedig

A C M ∢ = 90^{\circ} - C A T ∢ = 90^{\circ} - α

Megjegyzés. Ha a háromszög

γ

szöge tompaszög, akkor is teljesül, hogy

B C N ∢ = 90^{\circ} - α

, az

M

pont viszont a

T C

szakasz

C

-n túli meghosszabbításán van, ezért

A C M ∢ = 90^{\circ} + α

, tehát a feladat állítása nem igaz.