Feladat: Gy.2611 Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Adorján Richárd ,  Baksa Zsolt ,  Bánfalvi Koppány ,  Bánky Boróka ,  Berente Bálint ,  Bernáth Csaba ,  Bükki Csilla ,  Csekő Zoltán ,  Csikai Szabolcs ,  Czirják Gábor ,  Frankó Tamás ,  Gálig András ,  Gefferth András ,  Győry Máté ,  Harcos Gergely ,  Hegedűs Pál ,  Hegyi Zsuzsa ,  Honti Balázs ,  Horvai Péter ,  Horváth István ,  Jónás Veronika ,  K. L. ,  Molnár-Sáska Gábor ,  Tőke Csaba ,  Újváry-Menyhárt Zoltán ,  Veres Gábor ,  Veres Tamás ,  Virág Bálint ,  Waldhauser Tamás ,  Zsók Balázs 
Füzet: 1990/december, 458 - 459. oldal  PDF  |  MathML 
Témakör(ök): Beírt kör középpontja, A háromszögek nevezetes pontjai, Húrnégyszögek, Diszkusszió, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1990/február: Gy.2611

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a feladatot megoldottnak. Jelöljük a szerkesztendő háromszög csúcsait A,B,C-vel, beírt körének középpontját O-val, a hozzáírt körök középpontjait P,Q,R-rel, az OP,OQ,OR szakaszok felezőpontját pedig rendre X,Y,Z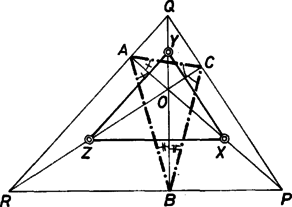-vel.

 
 

Tudjuk, hogy a beírt kör középpontja a három belső szögfelező, a hozzáírt körök középpontja pedig két külső és egy belső szögfelező metszéspontja. Ezért az A,O,X,P; B,O,Y,Q és C,O,Z,R pontnégyesek az ABC háromszög egy-egy belső szögfelezőjén, az R,A,Q ; P,B,R és Q,C,P ponthármasok pedig az ABC háromszög egy-egy külső szögfelezőjén helyezkednek el. Egy szög külső és belső szögfelezői egymásra merőlegesek, így AO⊥RQ, BP⊥PR és CO⊥QP. Mivel X,Y és Z felezőpontok, ezért ha a PQR háromszöget az O pontból felére kicsinyítjük, akkor az XYZ háromszöget kapjuk, tehát ennek a háromszögnek az oldalai párhuzamosak a PQR háromszög oldalaival. Az előzőekben belátott merőlegességekből következik, hogy AOX⊥ZY, BOY⊥XZ és COZ⊥YX, vagyis O az XYZ háromszög magasságpontja.
Ezek alapján a szerkesztés menete a következő : Az adott XYZ háromszögnek megszerkesztjük a magasságpontját, ami éppen a szerkesztendő háromszög beírt körének O középpontja. Ebből a pontból az XYZ háromszöget kétszeresére nagyítva kapjuk a PQR háromszöget, amelynek csúcsai a szerkesztendő háromszög hozzáírt köreinek középpontjai, oldalai pedig az ABC háromszög külső szögfelezői. Végül O-ból merőlegeseket bocsátunk a PQR háromszög oldalegyeneseire (ezek a merőlegesek éppen az ABC háromszög belső szögfelezői), e merőlegesek talppontjai adják a szerkesztendő háromszög csúcsait.
Az így szerkesztett ABC háromszög a PQR háromszög talpponti háromszöge, ezért OA, OB és OC valóban belső szögfelezők (ennek bizonyítása megtalálható pl. a Geometriai feladatok gyűjteménye I. 1060. feladatában), a merőlegességek miatt pedig PR, RQ és QP külső szögfelezők, tehát P,Q és R a hozzáirt körök középpontjai. Vagyis az ABC háromszög beírt körének középpontját a hozzáírt körök középpontjával összekötő szakaszok felezőpontjai éppen az X, Y és Z pontok.
Ha az XYZ háromszög hegyesszögű, akkor pontosan 1 megoldás van (ez következik a szerkesztésből). Ha az X,Y,Z pontok egy egyenesbe esnek, vagy ha az XYZ háromszög nem hegyesszögű, akkor nincs megoldás. (Az XYZ háromszög minden szöge hegyesszög, mert pl.
ZXY∢=BPC∢=COQ∢=OCB∢+OBC∢=ACB∢+CBA∢2<ACB∢+CBA∢+BAC∢2=180∘2=90∘. Közben felhasználtuk, hogy PBOC húrnégyszög.)
 
 Molnár-Sáska Gábor (Bp., Fazekas M. Gyak. Gimn., I. o. t.)
 dolgozata alapján