| Feladat: | Gy.2609 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Harcos Gergely , Veres Gábor | ||
| Füzet: | 1991/március, 103 - 105. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Gráfok összefüggősége, Algoritmikus eljárások, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1990/február: Gy.2609 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megoldás. Írjuk először a feladatban szereplő konvex poliéder minden élére a számot, és nevezzük a poliéder tetszőleges csúcsát -csúcsnak vagy -csúcsnak aszerint, hogy az oda befutó élekre írt számok szorzata vagy . Egyelőre tehát a poliéder minden csúcsa -csúcs, és azt kell belátnunk, hogy az élek megszámozhatók a és a számokkal úgy, hogy mindegyik csúcs -csúcs legyen. Nyilván elegendő megadnunk egy olyan algoritmust, amely ‐ feltéve, hogy van legalább darab csúcs pontosan -vel növeli a -csúcsok számát azáltal, hogy néhány élnél az ellentettjére változtatja a ráírt számot. Ha ui. ezt az algoritmust egymás után -szer alkalmazzuk, akkor lépésenként rendre lesz a -csúcsok száma, tehát végül valamennyi csúcs -csúcs lesz. 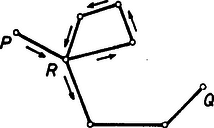 1.a) ábra: , amely tartalmaz ,,kétszeres'' csúcsot 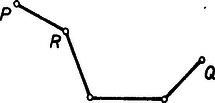 1.b) ábra: , amely -ből egy zárt töröttvonal elhagyásával keletkezett Feltevésünk szerint tehát a töröttvonalban a és pontokhoz pontosan ‐ él csatlakozik, a belső töréspontokhoz pedig pontosan . Változtassuk most az ellentettjére a -beli élekre írt számokat (2. ábra). 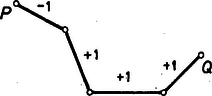 2.a) ábra: T az algoritmus alkalmazása előtt ( és csúcsok) 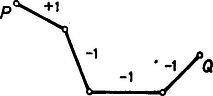 2.b) ábra: T az algoritmus alkalmazása után ( és csúcsok) Ekkor a és a csúcsok esetében pontosan a -szeresére, a belső töréspontok esetében pedig a -szeresére változik az oda befutó élekre írt számok szorzata. Az algoritmus nyilván nem befolyásolja a -hez nem tartozó csúcsokba futó élekre írt számokat, tehát valóban pontosan kettővel -vel és -val ‐ növeli a -csúcsok számát. Akkor is érvényes a meggondolás, ha a -ből -ba vezető töröttvonal egyes belső töréspontjai már egy korábbi lépésben -csúccsá változtak. Megjegyzés. Bizonyításunk közben a feladatbeli poliéder konvex voltából csak annyit használtunk fel, hogy a poliéder élhálózata összefüggő, azaz bármely két csúcsa összeköthető élekből álló töröttvonallal. Mivel ez az egyszerű poliéderekre is fennáll (lásd Hajós György: Bevezetés a geometriába, Tankönyvkiadó, Bp. 1987. 26‐28. oldal), továbbá a csúcsok számának helyett akármilyen más (-nél nem kisebb) páros számot is tekinthettünk volna, ezért igaz a feladat következő általánosítása: Egy páros csúcsszámú egyszerű poliéder élei megszámozhatók a és a számokkal úgy, hogy minden egyes csúcsra teljesül, hogy az oda befutó élekre írt számok szorzata . Ha nem törekszünk arra, hogy minden egyes csúcs esetében legyen az oda befutó élekre írt számok szorzata (tehát, hogy minden egyes csúcs -csúcs legyen), akkor tetszőleges egyszerű poliéderre kiterjeszthetjük az általánosítást: Ha egy egyszerű poliéder éleinek száma , akkor bármely páros számra megszámozhatók a poliéder élei a és a számokkal úgy, hogy pontosan legyen a -csúcsok száma (ebben az esetben az algoritmust -ször kell egymás után alkalmaznunk a megoldáshoz hasonló kiindulási helyzet után). Rögtön felvetődik a kérdés, hogy ‐ az előző jelöléseket használva ‐ tetszőleges egyszerű poliéder esetében van-e olyan páratlan szám, amelyre megszámozhatók a poliéder élei a és a számokkal úgy, hogy pontosan legyen a -csúcsok száma. Könnyen észrevehetjük, hogy nincs ilyen szám, ha ui. lenne, akkor sorra összeszorozva az egyes csúcsoknál az oda befutó élekre írt számok szorzatát, egyrészt -et kellene kapnunk, hiszen páratlan számú -csúcsunk van ( db), másrészt -et, mert a szorzás során minden egyes élre írt szám pontosan kétszer szerepelt tényezőként, és -ek ill. -ek szorzata valóban . Az eddigiek alapján tehát egy élű egyszerű poliéder esetében pontosan a páros számokra létezik olyan számozás, amelynél pontosan db -csúcs (ill. darab -csúcs) van. Harcos Gergely (Bp., ELTE Apáczai Csere J. Gimn., III. o. t.) |