Kezdőlap


Feladat:	Gy.2603	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Álmos Attila , Czirók András , Imreh Csanád , Lente Gábor
Füzet:	1990/december, 456 - 458. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Derékszögű háromszögek geometriája, Hatványközepek közötti egyenlőtlenség, Deltoidok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1990/január: Gy.2603

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először egy, a derékszögű háromszögekre vonatkozó egyenlőtlenséget bizonyítunk be:
(*) Ha $a$ és $b$ egy derékszögű háromszög befogói, $c$ pedig az átfogó, akkor

\begin{matrix} a + b < \frac{3}{2} c . \end{matrix}

1. ábra

Bizonyítás. Jelöljük

m

-mel a háromszög átfogóhoz tartozó magasságát. Ekkor

a \cdot b = m \cdot c

, hiszen mindkettő megegyezik a háromszög területének kétszeresével. Pitagorasz tétele szerint

a^{2} + b^{2} = c^{2}

tehát,

a^{2} + b^{2} < c^{2} + m^{2}

. Vagyis

\begin{matrix} a^{2} + b^{2} + 2 a b < c^{2} + m^{2} + 2 m c \end{matrix}

azaz

\begin{matrix} {(a + b)}^{2} < {(c + m)}^{2}, \end{matrix}

amiből ‐ pozitív számokról lévén szó ‐ következik, hogy

a + b < c + m

. Másrészt tudjuk, hogy

m < \frac{1}{2} c

(1. ábra), tehát

a + b < c + \frac{1}{2} c

; ezzel a (*) állítást beláttuk.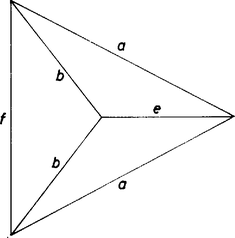

2. ábra

Térjünk vissza eredeti feladatunkra. Ha a deltoid konkáv, akkor állításunk triviális (a 2. ábra jelöléseivel:

e < a

f < 2 b < a + b

, tehát

e + f < 2 a + b

). Ha a deltoid konvex, akkor jelöljük oldalainak hosszát

a

-val és

b

-vel (

a ≧ b

), átlóit

e

-vel és

f

-fel úgy, hogy

e

felezi

f

-et,

f

pedig

e_{1}

és

e_{2}

hosszúságú részekre osztja

e

-t (3. ábra).

3. ábra

Az átlók a deltoidot négy derékszögű háromszögre bontják. A (*) állítást ezen háromszögekre alkalmazva kapjuk, hogy

\begin{matrix} e_{1} + \frac{f}{2} < \frac{3}{2} b, \end{matrix}

és

\begin{matrix} e_{2} + \frac{f}{2} < \frac{3}{2} a . \end{matrix}

Ezeket összeadva és felhasználva, hogy

a ≧ b

, kapjuk hogy

\begin{matrix} e + f = e_{1} + \frac{f}{2} + e_{2} + \frac{f}{2} < \frac{3}{2} a + \frac{3}{2} b ≦ 2 a + b \end{matrix}

ami éppen a bizonyítandó állítás.

Lente Gábor (Eger, Gárdonyi G. Gimn., II. o. t.)
dolgozata alapján

Megjegyzés. A (*) állítás a számtani és a négyzetes közép közti egyenlőtlenség felhasználásával egyszerűbben is bizonyítható:

\begin{matrix} \frac{a + b}{2} ≦ \sqrt[]{\frac{a^{2} + b^{2}}{2}} = \sqrt[]{\frac{c^{2}}{2}} = \frac{\sqrt[]{2} \cdot c}{2}, \end{matrix}

vagyis

a + b ≦ \sqrt[]{2} c

is igaz.