Kezdőlap


Feladat:	Gy.2580	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csorba P. , Csöre I. , Erben P. , Farkas Z. , Földesi P. , Illés Mariann , Katz S. , Kucsera H. , Lángi Zs. , Matolcsi M. , Miklós Gy. , Nemes N. , Schauermann T. , Ugrai P. , Vidács A. , Wiener G.
Füzet:	1990/április, 168 - 170. oldal		PDF \| MathML
Témakör(ök):	Menelaosz-tétel, Párhuzamos szelők tétele, Diszkusszió, Háromszögek szerkesztése, Vektorok lineáris kombinációi, Gyakorlat
Hivatkozás(ok):	Feladatok: 1989/október: Gy.2580

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tekintsük a feladatot megoldottnak. Jelöljük az $A B$ oldal felezőpontját $D$ -vel, a $B C$ oldal $B$ -hez közelebbi negyedelőpontját $E$ -vel, a $C A$ oldal $C$ -hez közelebbi nyolcadoló pontját pedig $F$ -fel. Rajzoljunk $F$ -en át párhuzamost a $B C$ oldallal. Messe ez a $D E$ szakaszt $J$ -ben, az $A B$ oldalt pedig $K$ -ban (1. ábr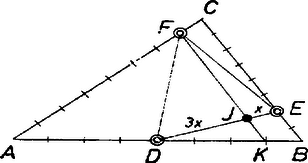a).

1. ábra

Mivel

C B ∥ F K

, ezért a párhuzamos szelők tétele szerint

A K : K B = A F : F C = 7 : 1

, tehát

K

nyolcadolópontja az

A B

oldalnak,

D

ugyanennek az oldalnak a felezőpontja, ezért

D K : K B = 3 : 1

. A párhuzamos szelők tételét az

E D B

szögre alkalmazva kapjuk, hogy

D J : J E = D K : K B = 3 : 1

. Tehát az

F

ponton át a

B C

oldallal húzott párhuzamos a

D E

szakaszt 3:1 arányban osztja. Teljesen hasonló módon láthatjuk be, hogy a

D

ponton át

A C

-vel húzott párhuzamos az

E F

szakaszt 1:2 arányban (2. ábra), az

E

ponton át

A B

-vel húzott párhuzamos az

F D

szakaszt pedig 5:2 arányban osztja (3. ábra).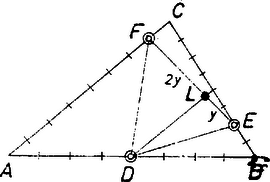

2. ábra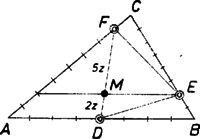

3. ábra

Ezek alapján a szerkesztést a következőképpen végezhetjük el:
A

D E

E F

és

F D

szakaszokon megszerkesztjük azokat a

J

L

M

pontokat, melyekre

D J : J E = 3 : 1

E L : L F = 1 : 2

és

F M : M D = 5 : 2

. Ezután

F J

-vel

E

-n át,

D L

-lel

F

-en át,

E M

-mel pedig

D

-n át párhuzamost húzunk. Ez a három párhuzamos a szerkesztendő háromszög három oldalegyenese.
Könnyen belátható ‐ a párhuzamos szelők tételének többszöri alkalmazásával ‐, hogy az így szerkesztett háromszögben a

D

E

F

pontok valóban felező-, negyedelő-, illetve nyolcadoló pontok. Ha a

D

E

F

pontok egy egyenesbe esnek, akkor a feladatnak nincs megoldása, minden más esetben egy megoldás van.

Illés Mariann (Tata, Eötvös J. Gimn., II. o. t.) dolgozata alapján

II. megoldás. A feladatot a következő, általánosabb formában oldjuk meg:
Szerkesszük meg az

A B C

háromszöget, ha adottak oldalegyenesein azok a

D

E

F

pontok, melyekre

A D : D B = 1 : α

B E : E C = 1 : β

és

C F : F A = 1 : γ

, ahol

α

β

és

γ

adott racionális számok.
Indítsunk a sík egy tetszőleges

O

pontjából helyvektorokat a szereplő pontokhoz, és jelöljük ezeket a megfelelő kisbetűvel. Ekkor az arányosan osztó pont helyvektorára vonatkozó ismert szabály alapján felírhatjuk, hogy:

\begin{matrix} d & = \frac{α a + b}{1 + α}, \\ e & = \frac{β b + c}{1 + β}, \\ f & = \frac{γ c + a}{1 + γ} . \end{matrix}

Ezt az egyenletrendszert

a, b, c

-re megoldva kapjuk, hogy:

\begin{matrix} a & = \frac{1}{1 + α β γ} (β γ (1 + α) d - γ (1 + β) e + (1 + γ) f), \\ b & = \frac{1}{1 + α β γ} ((1 + α) d + α γ (1 + β) e - α (1 + γ) f), \\ c & = \frac{1}{1 + α β γ} (- β (1 + α) d + (1 + β) e + α β (1 + γ) f) . \end{matrix}

A szerkesztést úgy végezzük, hogy a

d, e, f

vektorok ismeretében megszerkesztjük az

a, b, c

vektorokat, s ezeknek a végpontjai adják a háromszög csúcspontjait. (Eredeti feladatunkban

α = 1

β = 3

és

γ = 7

.)
A diszkusszió az általános esetben valamivel bonyolultabb. Ha a

D

E

F

pontok nincsenek egy egyenesen és

α β γ \neq - 1

, akkor egy megoldás van. Ha a

D

E

F

pontok egy egyenesen vannak és

α β γ = - 1

, akkor végtelen sok megoldás van, más esetben pedig nincs megoldás. (Ennek bizonyítását az érdeklődő olvasó Menelaosz tételének felhasználásával végezheti el.)

Megjegyzés: Természetesen az első megoldás módszerével is megoldható az általános feladat, ennek végiggondolását is az olvasóra bízzuk.