Feladat: Gy.2573 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Álmos A. ,  Búzás S. ,  Keresztély T. ,  Komócsi S. ,  Kórász T. ,  Nagypál Éva ,  Perlaki T. ,  Újváry-Menyhárt Zoltán ,  Varjú Katalin ,  Virág B. 
Füzet: 1990/november, 387 - 390. oldal  PDF  |  MathML 
Témakör(ök): Kocka, Kombinációk, Térgeometria alapjai, Gyakorlat
Hivatkozás(ok):Feladatok: 1989/szeptember: Gy.2573

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A síkokat a rájuk illeszkedő élfelezőpontok száma szerint fogjuk csoportosítani. Megmutatjuk, hogy az egyes síkokon 6, 4 vagy 3 élfelezőpont van, majd pedig meghatározzuk az egyes csoportokba tartozó síkok számát.
A kockának 6 lapja van, ezért egy tetszőleges sík legfeljebb 6 oldalú sokszögben metszi a kockát. Az élfelezőpontok a metszetsokszög határán helyezkednek el, mindegyik oldalon egy: ezért legfeljebb 6 élfelezőpont lehet egy síkon. Nevezzünk két élfelezőpontot szomszédosnak, ha a hozzájuk tartozó éleknek van közös csúcsuk.

 
 

1. ábra
 


Egyszerűen belátható, hogy ha egy sík legalább 5 élfelezőpontot tartalmaz, akkor azok közt vannak szomszédosak: (Minden élfelezőpontnak 4 szomszédja van. Ha az öt pont közül semelyik kettő nem lenne szomszédos, akkor az egyik kiválasztott pont 4 szomszédja közül egyik sem lehetne a kiválasztottak közt ‐ lásd az 1. ábra A, illetve B, H, K, F pontjait ‐, a maradék 12-5=7 pont közül pedig nyilván nem lehet 4-et úgy kiválasztani, hogy azok közül semelyik kettő sem szomszédos.) Tegyük fel először, hogy az S síkon legalább 5 élfelezőpont van. Ekkor ezek között van két szomszédos. Legyenek ezek ‐ a 2. ábra jelöléseit használva ‐ A és B. Ha a C pont is az S síkon van, akkor BC és AD párhuzamossága miatt (mindkettő párhuzamos az XY lapátlóval) a D pont is, CD és BE párhuzamossága miatt az E pont is, EF és AD párhuzamossága miatt az F pont is az S síkon van. Ez a sík tehát 6 élfelezőpontot tartalmaz, és könnyen látható, hogy merőleges a VZ testátlóra (lásd pl. Geometriai feladatok gyűjteménye I., 1851. feladat).
 
 

2. ábra
 

 
 

3. ábra
 

Ha az S sík nem tartalmazza a C pontot ‐ s így a D,E, F pontokat sem -, akkor több lehetőséget kell megvizsgálnunk. Ha S tartalmazza a ‐ 3. ábra jelöléseit használva ‐ a G vagy a H pontot, akkor megegyezik a kocka egyik lapsíkjával, s így éppen 4 élfelezőpontot tartalmaz. Ekkor S párhuzamos a kocka XZ élével és 4 élfelezőpontot tartalmaz. Az eddig tárgyaltakon kívül már csak két élfelezőpont, K és L van, tehát S semmiképpen sem tartalmazhat 5 élfelezőpontot. Vagyis a 6 élfelezőpontot tartalmazó sík merőleges a kocka egyik testátlójára, s mivel a testátlók száma 4, ezért 4 ilyen sík van. 5 élfelezőpontot tartalmazó sík pedig nem létezik.
Ha az S sík 4 élfelezőpontot tartalmaz és az élfelezőpontok közt vannak szomszédosak, akkor, mint már láttuk, két lehetőség van: vagy a kocka egyik lapsíkjáról van szó, ilyen sík 6 darab van; vagy pedig a kocka egyik élével párhuzamos síkról ‐ pl. a 3. ábra jelöléseivel az ABIJ sík ‐, ilyen sík 12 db van, a kocka 12 élére 1‐1.
 
 

4. ábra
 


Amennyiben a 4 élfelezőpont közül semelyik kettő nem szomszédos, úgy könnyen belátható, hogya 4 pont vagy a 4. ábrán látható A, G, D, J, vagy pedig az ugyanezen az ábrán látható A, J, C, L pontok mintájára helyezkedik el. (Tehát 2‐2 pont a kocka két szemközti lapján.) Az A, G, D, J pontok egy síkban vannak, ez a sík merőleges a kocka négy élére, ezért ilyen típusú síkokból 3db van. Az A, J, C és L pontok viszont nincsenek egy síkban. Összefoglalva: 6+12+3=21 olyan sík van, amely egy kockának pontosan 4 élfelezőpontját tartalmazza.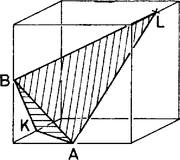
 
 

5. ábra
 

Ha az S sík pontosan 3 élfelezőpontot tartalmaz, és ezek közt vannak szomszédosak, akkor, mint már láttuk, két lehetőség van: vagy ‐ az 5. ábra jelöléseit használva ‐ az A,B és K pontokat tartalmazza a sík, vagy pedig az A, B és L pontokat. Az első típusú sík a kocka egyik csúcsát ,,vágja le'', ilyen síkból 8db van. A második típusú síkból minden szomszédos A, B párhoz pontosan egy tartozik, nevezetesen az a sík, amelynek harmadik élfelezőpontja annak az élnek a felezőpontja, amely A és B közös lapsíkjára merőleges és A-tól és B-től vett távolságainak összege a lehető legnagyobb. Minden oldallapon négy szomszédos pontpár van, ezért az ilyen típusú síkok száma 6⋅4=24. A továbbiakban két élfelezőpontot nevezzünk szemköztinek, ha a kockának ugyanazon a lapján vannak, de nem szomszédosak. Megmutatjuk, hogy ha az S sík pontosan 3 élfelezőpontot tartalmaz és azok közt nincsenek szomszédosak, akkor vannak szemköztiek.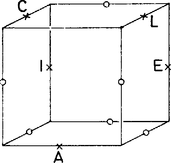
 
 

6. ábra
 


Egy élfelezőpont szomszédainak és szemközti pontjainak a száma 4+2=6, a maradék 12-(1+6)=5 pont közül kettőt kiválasztani úgy, hogy azok se szomszédosak, se szemköztiek ne legyenek, csak a 6. ábrán látható módon A, C, E vagy A, I, L lehet, ezek a síkok viszont nem 3, hanem 6 élfelezőpontot tartalmaznak, amint azt a megoldás során korábban már láttuk. Tehát feltehetjük, hogy az S sík tartalmazza az egymással szemközti A és J élfelező pontokat (7. ábra).
 
 

7. ábra
 


Az előzőek során beláttuk, hogy ha S a C vagy az L pont kivételével valamelyik másik élfelezőpontot tartalmazza, akkor S pontosan 4 élfelezőpontot tartalmaz. Tehát az S-re illeszkedő harmadik pont csak C vagy L lehet. Így minden szemközti pontpárhoz 2 sík tartozik. Minden lapon két szemközti pontpár van, ezek mindegyikéhez különböző síkok tartoznak, ezért az ilyen típusú síkok száma 2⋅2⋅6=24. Összesen tehát 8+24+24=56 olyan sík van, amely pontosan 3 élfelezőpontot tartalmaz.
Összegezve: 4+21+56=81 olyan sík van, amely egy kockának legalább 3 élfelezőpontját tartalmazza.
Megjegyzés. Kombinatorikai ismereteket felhasználva a 6, illetve 4 élfelezőpontot tartalmazó síkok számának meghatározása után a feladatot a következő, rövidebb módon is befejezhetjük: A 12 élfelezőpont (123)=220 háromszöget határoz meg. Azokon a síkokon, amelyeken 6 pont van, (63)=20 háromszög található, a 4 élfelezőpontot tartalmazó síkokon pedig (43)=4 háromszög. Tehát a pontok által meghatározott síkok száma: 220-4[(63)-1]-21[(43)-1]=81.