Kezdőlap


Feladat:	Gy.2571	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Molnár-Sáska G. , Nagy 999 Judit , Nográdi Z. , Szendrői B. , Tóth 875 Cs.
Füzet:	1990/április, 162. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Köréírt alakzatok, Négyzetek, Négyszögek középvonalai, Gyakorlat
Hivatkozás(ok):	Feladatok: 1989/szeptember: Gy.2571

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tulajdonképpen azt kell bizonyítanunk, hogy az $A B G E$ négyszög oldalainak felezőpontjai egy négyzetet határoznak meg. Ehhez először megmutatjuk, hogy ha egy négyszög két átlója merőleges és egyenlő hosszú, akkor a négyszög oldalfelező pontjai négyzetet határoznak meg, majd pedig belátjuk, hogy az $A G$ és a $B E$ szakaszok egymásra merőlegesek és egyenlő hosszúak.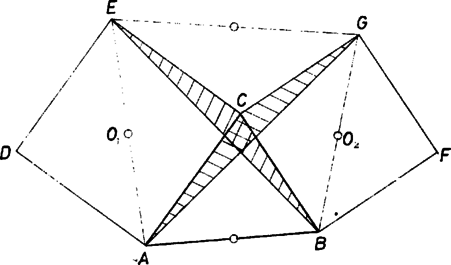

1. ábra

Legyen

P Q R S

tetszőleges olyan négyszög, amelynek átlói merőlegesek és egyenlő hosszúak. Megmutatjuk, hogy a négyszög

T

U

V

Z

oldalfelező pontjai négyzetet alkotnak (2. ábra).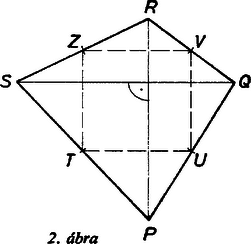

2. ábra

T U

U V

V Z

és

Z T

szakaszok rendre középvonalak a

P Q S

P Q R

Q R S

és

R S P

háromszögekben. Mivel egy háromszög középvonala fele olyan hosszú, mint a hozzá tartozó oldal, és azzal párhuzamos is, ezért egyrészt

T U = V Z = \frac{1}{2} Q S = \frac{1}{2} P R = U V = Z T

, másrészt

Z T U ∢ = 90^{\circ}

, hiszen megegyezik a

P R

és

Q S

egyenesek szögével. Tehát a

T U V Z

négyszög négyzet.
Eredeti feladatunkhoz visszatérve tekintsük az

A G C

és az

E B C

háromszögeket (1. ábra). Mivel

A C E D

és

C B F G

négyzet, ezért a

C

pont körüli

90^{\circ}

-os elforgatás a

C E

szakaszt

C A

-ba,

C B

-t pedig

C G

-be viszi, azaz a

C E B

háromszög az elforgatás során a

C A G

háromszögbe megy át. Ez viszont azt jelenti, hogy a háromszögek harmadik oldalai ‐

B E

és

A G

‐ is egyenlő hosszúak és egymásra merőlegesek. Tehát az

A B G E

négyszögre alkalmazhatjuk előző eredményünket, amiből feladatunk állítása következik.