Kezdőlap


Feladat:	Gy.2564	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Nagy Judit
Füzet:	1990/február, 70 - 71. oldal		PDF \| MathML
Témakör(ök):	Szögfelező egyenes, Körök, Gyakorlat
Hivatkozás(ok):	Feladatok: 1989/május: Gy.2564

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az adott háromszög csúcsait és oldalait a szokásos módon $A$ , $B$ , $C$ , illetve $a$ , $b$ , $c$ -vel. Az $A$ -ból induló belső, illetve külső szögfelezőnek a $B C$ egyenessel való metszéspontja legyen $F_{A}$ , illetve $G_{A}$ . Az $F_{A} G_{A}$ szakaszra mint átmérőre rajzolt kör legyen $k_{A}$ . Hasonló módon kapjuk a $k_{B}$ és $k_{C}$ kör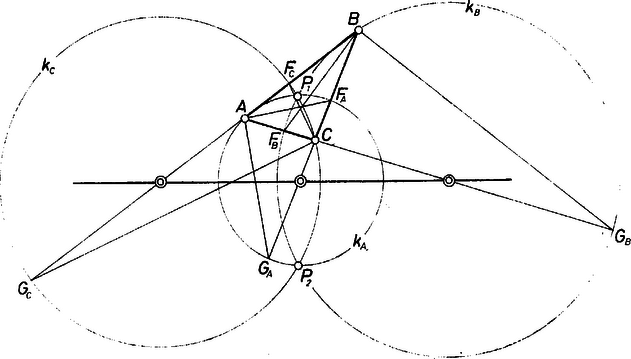öket.
Ismeretes (lásd pl.: Geometriai feladatok gyűjteménye I.), hogy $k_{A}$ a $B$ és $C$ pontokhoz és a $\frac{c}{b}$ arányhoz tartozó Apollóniusz-kör, vagyis azoknak a $P$ pontoknak a mértani helye, amelyekre $\frac{P B}{P C} = \frac{c}{b}$ . Hasonlóan a $k_{B}$ , illetve a $k_{C}$ azon $Q$ , illetve $R$ pontok mértani helyei, melyekre $\frac{Q C}{Q A} = \frac{a}{c}$ , illetve $\frac{R A}{R B} = \frac{b}{a}$ .
Tekintsük a $k_{A}$ és $k_{B}$ körök $P_{1}$ és $P_{2}$ metszéspontjait, (Később megmutatjuk, hogy ez a két metszéspont mindig létezik.) Ezekre:

\begin{matrix} \frac{P_{i} B}{P_{i} C} = \frac{c}{b} és \frac{P_{i} C}{P_{i} A} = \frac{a}{c} . \end{matrix}

Tehát

\begin{matrix} \frac{P_{i} B}{P_{i} A} = \frac{a}{b} (i = 1, 2), \end{matrix}

vagyis ez a két pont rajta van

k_{C}

-n is. Tehát a

P_{1} P_{2}

szakasz mind a három körnek húrja. Ez azt jelenti, hogy a

P_{1} P_{2}

szakasz felező merőlegesén mind a három körnek a középpontja rajta van. E három középpont pedig éppen a feladatunkban szereplő három pont.

Azt kell még megmutatnunk, hogy a három kör közül valamelyik kettő metszi egymást. Feltehetjük, hogy

β

a háromszög legkisebb szöge. Ekkor

G_{A}

B C

oldal

C

-n túli,

G_{C}

pedig a

B A

oldal

A

-n túli meghosszabbításán van, vagyis

C

F_{A} G_{A}

A

pedig az

F_{C} G_{C}

átmérőn. Tehát

C

k_{C}

körvonal egyik pontja) belső pontja

k_{A}

-nak.

A

k_{A}

egyik pontja) pedig belső pontja

k_{C}

-nek. Ebből nyilvánvalóan következik, hogy a

k_{A}

és

k_{C}

körök metszik egymást.
Ezzel a feladatot megoldottuk.

Nagy Judit (Miskolc, Földes F. Gimn., I. o. t.)
dolgozata alapján