Kezdőlap


Feladat:	Gy.2563	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Újváry-Menyhárt Zoltán
Füzet:	1990/október, 306 - 307. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Magasságvonal, Szögfelező egyenes, Körülírt kör, Gyakorlat
Hivatkozás(ok):	Feladatok: 1989/május: Gy.2563

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy az $e_{A}$ , $e_{B}$ , $e_{C}$ egyenesek mindegyike átmegy az $A B C$ háromszög köré írható kör $O$ középpontján. Elegendő belátnunk, hogy az $e_{A}$ egyenes átmegy az $O$ ponton, a másik két egyenesre a bizonyítás hasonlóan végezhető el.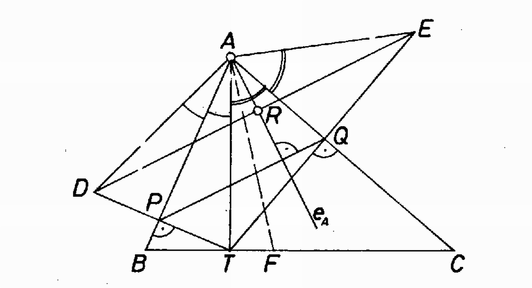

1. ábra

Jelöljük az

A

-ból induló magasság talppontját

T

-vel, az

A

csúcshoz tartozó belső szögfelező és

B C

metszéspontját

F

-fel. Először azt bizonyítjuk be, hogy az

e_{A}

egyenes megegyezik az

A T

egyenes

A F

-re vonatkozó tükörképével. Jelöljük a

T

pont

P

-re, illetve

Q

-ra vonatkozó tükörképét

D

-vel, illetve

E

-vel.

e_{A}

és

D E

metszéspontját pedig

R

-rel (1. ábra). Azt kell belátnunk, hogy

T A R ∢ = 2 T A F ∢

. A

P Q

szakasz középvonal a

T D E

háromszögben, ezért

D E

párhuzamos

P Q

-val, vagyis

e_{A}

D E

-re is merőleges. Az

A T

szakasz

A B

-re vonatkozó tükörképe

A D

A C

-re vonatkozó tükörképe pedig

A E

, ezért az

A D E

háromszögben

A D = A E

. Továbbá

D A E ∢ = D A T ∢ + T A E ∢ = 2 B A T ∢ + 2 T A C ∢ = 2 B A C ∢

. Tudjuk, hogy

A R

merőleges

D E

-re, ezért

A R

felezi az

A D E

egyenlő szárú háromszög

A

-nál levő szögét, vagyis

D A R ∢ = \frac{1}{2} D A E ∢ = B A C ∢ = 2 B A F ∢

. Ezeket az összefüggéseket felhasználva:

\begin{matrix} T A R ∢ = D A R ∢ - D A T ∢ = 2 B A F ∢ - 2 B A T ∢ = 2 (B A F ∢ - B A T ∢) = \\ = 2 T A F ∢ . \end{matrix}

Ezzel beláttuk, hogy az

e_{A}

egyenes valóban az

A

-hoz tartozó magasságvonalnak az

A

-hoz tartozó belső szögfelezőre vonatkozó tükörképe. Most bebizonyítjuk, hogy ez a tükörkép mindig átmegy az

O

ponto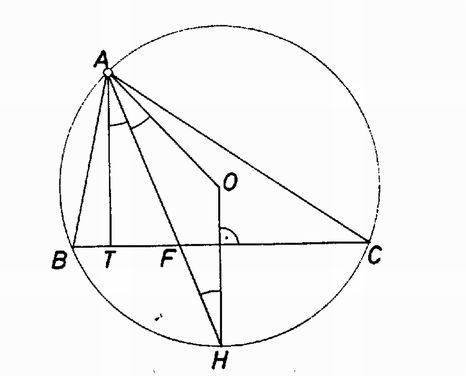n.

2. ábra

Ismert (lásd pl. Geometriai feladatok gyűjteménye I., 968. feladat), hogy az

A F

egyenes és a

B C

oldal felező merőlegese ugyanabban az

M

pontban metszi a háromszög köré írt (

O

középpontú) kört ‐

M

B C

ív felezőpontja (2. ábra). Az

O A

és az

O M

szakaszok a köré írt kör sugarai, ezért az

O A M

háromszög egyenlő szárú, tehát

O A M ∢ = O M A ∢

. Másrészt

A T

is és

O M

is merőleges a

B C

oldalra, ezért a

T A M ∢

és az

O M A ∢

váltószögek. Így

O A M ∢ = T A M ∢

, tehát

A T

-nek

A M

-re vonatkozó tükörképe átmegy

O

-n.

Ujváry‐Menyhárt Zoltán (Budapest, Fazekas M. Gimn., I. o. t.)
dolgozata alapján.