Kezdőlap


Feladat:	Gy.2555	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Antos A. , Balogh 171 J. , Benczúr P. , Bérczes A. , Botrágyi T. , Csirik J. , Erős Krisztina , Fleiner B. , Harcos G. , Horváth I. , Imreh Cs. , Ittzés D. , Katsányi I. , Kovács 998 P. , Macskási Zs. , Molnár-Sáska G. , Nagy Judit , Németh S. , Perlaki T. , Podoski Károly. , Rijsbjerg Anna , Szalkai Á. , Szendrődi B. , Szőllősy G. , Virág B.
Füzet:	1990/március, 116 - 117. oldal		PDF \| MathML
Témakör(ök):	Menelaosz-tétel, Négyszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1989/április: Gy.2555

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Felhasználjuk a következő ‐ Menelaosz tétele néven ismert ‐ állítást: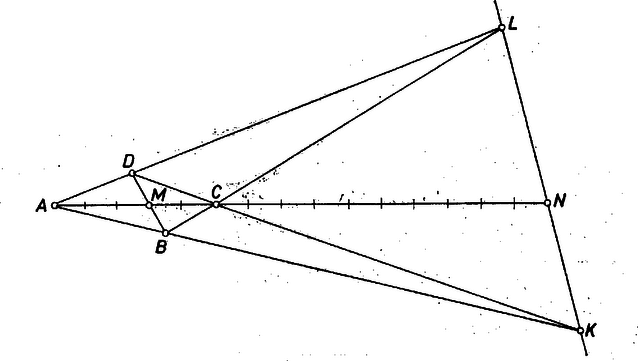
(1) Az $A B C$ háromszög $A B$ , $B C$ , $C A$ oldalegyeneseire illeszkedő ‐ csúcsoktól különböző ‐ $X$ , $Y$ , $Z$ pontok pontosan akkor vannak egy egyenesen, ha az irányított szakaszokra fennáll, hogy:

\begin{matrix} \frac{A X}{X B} \cdot \frac{B Y}{Y C} \cdot \frac{C Z}{Z A} = - 1. \end{matrix}

(Ennek bizonyítása megtalálható pl. a Geometriai feladatok gyűjteménye I. 1260. feladatában.)

Alkalmazzuk (1)-et először a

B M A

háromszögre és a

K

C

D

pontokra, majd a

B C A

háromszögre és a

K

N

L

pontokra, végül a

B C M

háromszögre és az

L

A

D

pontokra:

\begin{matrix} \frac{B D}{D M} \cdot \frac{M C}{C A} \cdot \frac{A K}{K B} = - 1, \\ \frac{B K}{K A} \cdot \frac{A N}{N C} \cdot \frac{C L}{L B} = - 1, \\ \frac{B L}{L C} \cdot \frac{C A}{A M} \cdot \frac{M D}{D B} = - 1. \end{matrix}

Ezeket összeszorozva és a lehetséges egyszerűsítéseket elvégezve kapjuk, hogy:

\begin{matrix} \frac{A N}{N C} \cdot \frac{M C}{A M} = - 1, azaz \frac{C N}{A N} = \frac{M C}{A M} = \frac{2}{3} . \end{matrix}

Ebből:

3 C N = 2 A N = 2 (A C + C N)

, vagyis

C N = 2 A C = 2 (A M + M C) = 10

cm.

Nagy Judit (Miskolc, Földes F. Gimn., I. o. t.)