Feladat: Gy.2548 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Köszegi Botond 
Füzet: 1990/november, 385 - 387. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Diszkusszió, Síkgeometriai szerkesztések, Gyakorlat
Hivatkozás(ok):Feladatok: 1989/március: Gy.2548

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a feladatot megoldottnak. Az adott háromszög csúcsait jelöljük A, B, C-vel, szögeit α, β, γ-val, a szerkesztendő pontot P-vel, P-nek a háromszög oldalegyenesein lévő merőleges vetületeit pedig A1, B1, C1-gyel. A háromszög oldalegyenesei a síkot hét részre osztják. Számozzuk meg ezeket az 1. ábrán látható módon. Háromféle esetet kell megkülönböztetnünk attól függően, hogy P-t melyik síkrészben helyezkedik el.

 
 

1. ábra
 

 
I. eset: P az 1. síkrészben ‐ a háromszög belsejében ‐ van. Ekkor az AB1PC1, BC1PA1 és CA1PB1 négyszögekben két-két egymással szemközti derékszög található (2. ábra), tehát B1PC1∢=180∘-α, C1PA1∢=180∘-β és A1PB1∢=180∘-γ.
 
 

2. ábra
 

Ezt felhasználva a szerkesztést a következő módon végezhetjük el: Felveszünk egy tetszőleges A'1B'1C'1 szabályos háromszöget. Megszerkesztjük az A'1B'1 szakasz 180∘-γ szögű és a B'1C'1 szakasz 180∘-α szögű látóköríveit. Ezeknek az A'1B'1C'1 háromszög belsejében lévő metszéspontját jelöljük P'-vel. A P'A'1, P'B1, P'C1 szakaszokra a P'-től különböző végpontjukban merőlegeseket állítunk. Ezek metszéspontjait jelöljük A', B', C'-vel. Ekkor B'A'C'∢=C'1A'B'1∢=360∘-(P'C'1A'∢+B'1P'C'1∢+A'B'1P'∢)=360∘-(90∘+(180∘-α)+90∘)=α, és ugyanígy A'B'C'∢=β, B'C'A'∢=γ. Tehát az A'B'C' háromszög hasonló az ABC háromszöghöz. Az A'B'C' háromszöget (és vele együtt a P' pontot és az A'1B'1C'1 háromszöget is) megfelelően nagyítva az ABC háromszöggel egybevágó háromszöget kapunk, és ebből a háromszögből már csak át kell másolni a P' pont képét az eredeti háromszögbe. Az így szerkesztett P pont nyilván eleget tesz a feltételeknek.
 
 

3. ábra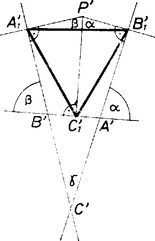
 

 
II. eset: P a 2., 3. vagy a 4. síkrészben van. A szerkesztés lényegében megegyezik az első esetben leírtakkal, csak a B1PC1, C1PA1, A1PB1 szögek közül kettő megegyezik az ABC háromszög egy-egy szögével, míg a harmadik az ABC háromszög egyik szögét 180∘-ra egészíti ki (pl. a 3. ábrán B1PC1∢=180∘-B1AC1∢=180∘-α, hiszen B1PC1A húrnégyszög, valamint C1PA1∢=C1BA1∢=β, A1PB1∢=A1CB1∢=γ, mivel ezek a szögek a BPC1A1, illetve a CPB1A1 húrnégyszögekben azonos ívhez tartozó kerületi szögek). Ezeknek a szögeknek az ismeretében egy tetszőleges szabályos háromszögből kiindulva a szerkesztendőhöz hasonló ábrát tudunk készíteni, s ezt megfelelően nagyítva meg tudjuk szerkeszteni a P pontot.
 
III. eset: P az 5., 6. vagy a 7. síkrészben van. Ekkor is az előzőekben leírtak szerint járunk el, most a B1PC1, C1PA1, A1PB1 szögek közül kettő ismét megegyezik az ABC háromszög egy-egy szögével, egy pedig 180∘-ra egészíti ki az ABC háromszög harmadik szögét. (A 4. ábrán pl. B1PC1∢=α, C1PA1∢=β és A1PB1∢=180∘-γ.)
 
 

4. ábra
 

Az I. esetben akkor kapunk megoldást, ha a 180∘-α, 180∘-β és 180∘-γ szögű látókörívek az A'1B'1C'1 háromszög belsejében metszik egymást. Mivel az A'1B'1C'1, háromszög minden szöge 60∘-os, ezért ez pontosan akkor teljesül, ha 180∘-α>60∘,180∘-β>60∘ és 180∘-γ>60∘, vagyis ha az eredeti háromszög minden szöge kisebb 120∘-nál. A II. esetben akkor kapunk megoldást (3. ábra), ha a B1PC1 szög 120∘-nál kisebb. Ha ugyanis a szög 120∘, akkor a szerkesztés során az A'B'C' háromszög csúcsai egybeesnek (5. ábra), ha pedig 120∘-nál nagyobb, akkor a P' pont az A'B'C' háromszög oldalegyenesei által meghatározott síkrészek közül nem a 2.-ba, hanem az azzal ,,szemben lévő'' 5.-be esik (6. ábra).Tehát a 2., 3. és 4. síkrészben akkor kapunk megoldást, ha rendre α>60∘, β>60∘, illetve γ>60∘. Ugyanígy látható be, hogy az 5., 6., illetve 7. részben pedig akkor van megoldás, ha 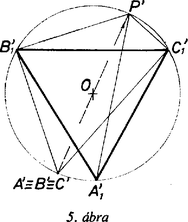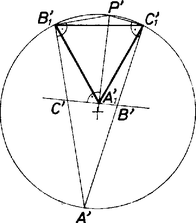α<60∘, β<60∘, illetve γ<60∘.
 
 

 
 

6. ábra
 

Összefoglalva : ha az ABC háromszögnek nincs 60∘-os szöge, akkor a 2.‐5., 3.‐6. és 4.‐7. síkrészpárok mindegyikében 1-1 megoldás van. Ha minden szög 120∘-nál kisebb, akkor az 1. síkrészben is van megoldás, ekkor tehát összesen négy megoldás van, ha viszont létezik 120∘-nál nagyobb szög, akkor csak három. Ha azABC háromszögnek egyetlen 60∘-os szöge van, akkor az egyik síkrészpárban nincs megoldás, az 1. síkrészben viszont igen, így a megoldások száma ekkor is három. Ha az ABC háromszög szabályos, akkor csak az 1. síkrészben van egyetlen megoldás.
 

Kőszegi Botond (Bp., Fazekas M. Gyak. Gimn., I. o. t.)

dolgozata alapján