Kezdőlap


Feladat:	Gy.2532	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	András Szilárd
Füzet:	1990/november, 384 - 385. oldal		PDF \| MathML
Témakör(ök):	Magasságpont, Gyakorlat
Hivatkozás(ok):	Feladatok: 1989/január: Gy.2532

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A megoldás során felhasználjuk a pont körre vonatkozó hatványának, valamint két kör hatványvonalának fogalmát, és ezek alapvető tulajdonságait. Az ezzel kapcsolatos definíciók és állítások megtalálhatók pl. a Geometriai feladatok gyűjteménye II. 923. és 931. feladatában.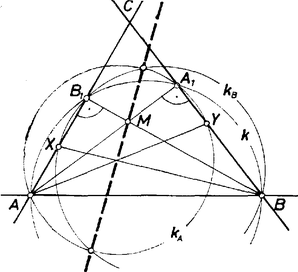
Először bebizonyítunk egy segédtételt:
$(*)$ Legyen $X$ és $Y$ az $A B C$ háromszög $A C$ , illetve $B C$ oldalegyenesének tetszőleges pontja. Ekkor az $A Y$ és a $B X$ átmérőjű körök hatványvonala tartalmazza az $A B C$ háromszög $M$ magasságpontját.

1. ábra

Jelöljük az

A B C

háromszög

A

-hoz, illetve

B

-hez tartozó magasságának talppontját

A_{1}

-gyel, illetve

B_{1}

-gyel, az

A Y

és a

B X

átmérőjű köröket pedig

k_{A}

-val és

k_{B}

-vel (1. ábra). Ekkor

A A_{1} Y ∢ = B B_{1} X ∢ = 90^{\circ}

, ezért az

A_{1}

pont rajta van a

k_{A}

, a

B_{1}

pont pedig a

k_{B}

körön; továbbá az

A_{1}

és a

B_{1}

pont rajta van az

A B

átmérőjű

k

körön. Ezért az

M

pontnak a

k_{A}

és a

k_{B}

körre vonatkozó hatványa

M A \cdot M A_{1}

és

M B \cdot M B_{1}

megegyezik, mert mindkettő egyenlő az

M

pont

k

-ra vonatkozó hatványával. Vagyis

M

rajta van a két kör hatványvonalán.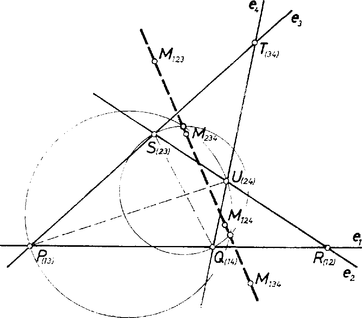

2. ábra

Térjünk rá az eredeti feladatunk megoldására. Jelöljük a 4 egyenes 6 metszéspontját a 2. ábrán látható módon

P

Q

R

S

T

U

-val. Válasszunk ki a 6 metszéspont közül 2-2 szemköztit ‐ azaz olyanokat, amelyek nincsenek egy egyenesen ‐, ábránkon

P

U

-t és

S

Q

-t. Azt állítjuk, hogy a

P U

és az

S Q

átmérőjű körök hatványvonala tartalmazza mind a négy magasságpontot. Ez segédtételünkből következik, ha azt négyszer alkalmazzuk az alábbi választásokkal:

\begin{matrix} \begin{matrix} 1. & 2. & 3. & 4. \\ A : & P & P & S & Q \\ B : & S & Q & U & U \\ C : & R & T & T & R \\ X : & Q & S & P & P \\ Y : & U & U & Q & S \end{matrix} \end{matrix}

Ezzel feladatunk állítását bebizonyítottuk.

András Szilárd (Csíkszereda, Matematika‐Fizika Líceum., I. o. t.)

dolgozata alapján