Feladat: Gy.2529 Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1990/január, 16 - 17. oldal  PDF  |  MathML 
Témakör(ök): Konstruktív megoldási módszer, Teljes indukció módszere, Gyakorlat
Hivatkozás(ok):Feladatok: 1989/január: Gy.2529

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az n-re vonatkozó teljes indukcióval bizonyítjuk az állítást. Ha n=1, akkor az 1. ábra táblázata megfelelő.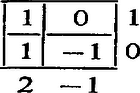

 
 

1. ábra
 

Legyen n≧1, és tegyük fel, hogy létezik olyan 2n×2n-es táblázat, amelyben az oszlopösszegek a
2n,-2n+1,2n-2,...,2,-1,
a sorösszegek pedig a
2n-1,-2n+2,2n-3,...,-2,1,0
számok. (Tehát a -2n hiányzik.) Illesszük ennek jobb alsó sarkához az 1. ábra táblázatát, és egészítsük ki két darab 2n×2n-es "szegéllyel'' a 2. ábrán látható módon.
Így a pozitív összegek 2-vel nőnek, a nem pozitívak 2-vel csökkennek, az 1. ábra sor- és oszlopösszegei tehát éppen "kitöltik a keletkezett hézagot'', a kapott (2n+2)×(2n+2)-es táblázat megfelelő lesz.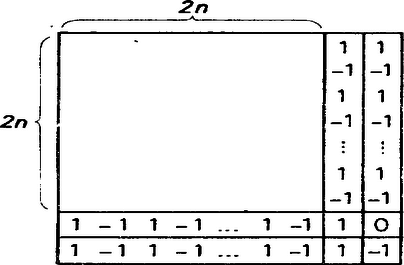
 
 

2. ábra
 

II. megoldás. Megadunk egy megfelelő kitöltést. A főátló első n darab eleme legyen 0, a második n elem legyen 1, a főátló alatti elemek értéke legyen -1, fölötte pedig (+1) értékek álljanak (3. ábra).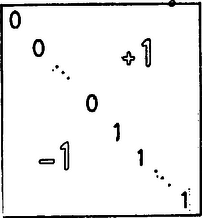
 
 

3. ábra
 

Ekkor az első n sorban különböző pozitív páratlan számok, a második n sorban pedig különböző nempozitív páros számok állnak. Az első n oszlopban különböző negatív páratlan számok, a második n oszlopban pedig különböző pozitív páros számok állnak.
Így valóban nincsenek egyenlők a 4n darab összeg között, hiszen bármelyik kettőnek különbözik vagy az előjele, vagy a paritása, vagy pedig az abszolút értéke.