Feladat: Gy.2524 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Czirók András ,  Végső Viktor 
Füzet: 1989/szeptember, 263 - 265. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Egyenlőtlenségek, Háromszögek nevezetes tételei, Terület, felszín, Paralelogrammák, Egyéb sokszögek geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1988/december: Gy.2524

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először a következő állítást igazoljuk:

Egy háromszögben elhelyezkedő paralelogramma területe legfeljebb fele(1)a háromszög területének.
Az állítás bizonyításához a befoglaló háromszöget kicsinyíthetjük, a paralelogrammát pedig úgy változtathatjuk, hogy területe ne csökkenjen. Így elérhetjük, hogy a területek között kívánt egyenlőtlenséget csupán nagyon speciális módon elhelyezkedő paralelogrammákra kelljen belátnunk.
 
 
1. ábra
 

A paralelogramma csúcsain keresztül párhuzamosakat húzunk a háromszög oldalaival (1. ábra). Ennek nyomán feltehetjük, hogy a paralelogrammának legalább három csúcsa a háromszög kerületén helyezkedik el. Tegyük fel, hogy ez a három csúcs mind különböző oldalon van, esetünkben P az AC,Q a BC,R pedig az AB oldalon. A PS félegyenes az AB oldalt S'-ben metszi, és ekkor a Q ponton átmenő, AB-vel párhuzamos egyenes metszi a PS' szakaszt P'-ben. Mivel a kapott P'QRS' paralelogramma területe megegyezik PQRS területével, feltehető, hogy a vizsgált paralelogramma két csúcsa (a 2. ábrán R és S) egyetlen oldalon (AB) fekszik, és még egy csúcs van a háromszög kerületén (Q a BC oldalon).
 
 
2. ábra
 

Használjuk a 2. ábra jelöléseit, a QP félegyenes metszi az AC oldalt a P* pontban, az AC-vel Q-n keresztül húzott párhuzamos pedig az AB oldalt metszi R*-ban. Mivel a PQ szakasz P*Q szakaszon fekszik, a P*QR*A paralelogramma területe legalább akkora, mint a PQRS területe. A továbbiakban tehát elegendő olyan paralelogrammákkal foglalkoznunk, amelyeknek egyik csúcsa A, és P,Q,R csúcsaik rendre az AC,CB, BA oldalakra illeszkednek (3. ábra).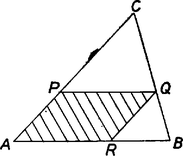
 
 
3. ábra
 

 A QRB és CPQ háromszögek hasonlóak CAB-hez, hiszen a megfelelő oldalaik párhuzamosak; jelölje a megfelelő szakaszok arányát α, ill. β. Mivel CQ+QB=CB, ezért α+β=1. Legyen az ABC háromszög területe t, ekkor a QRB ill. CPQ háromszögek területe α2t, ill. β2t, tehát a PQRA paralelogramma területe:
TPQRA=(1-α2-β2)t=2αβt≦(α+β)22t=12t;
ezzel az (1) állítást bebizonyítottuk.
Eredeti feladatunk állítása nyilvánvalóan igaz, ha valamelyik három pont elfajuló háromszöget határoz meg, ennek alapján feltehető, hogy az öt pont közül semelyik három sem esik egy egyenesbe.
Megmutatjuk, hogy ekkor a pontok között van négy olyan, amely konvex négyszöget határoz meg. Ha a pontok konvex burka ötszög, vagy négyszög, akkor a konvex burok (bármelyik) négy csúcsa megfelelő.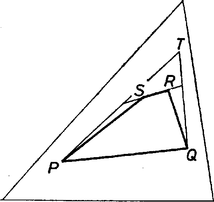
 
 
4. ábra
 

Tegyük fel, hogy pontjaink konvex burka a PQT háromszög (4. ábra). A másik két pont, R és S által meghatározott egyenes PQT-nek pontosan két oldalát metszi, legyenek ezek például TP és TQ. Ekkor a P,Q,R,S pontok konvex négyszöget határoznak meg.
Mivel a négyszög szögeinek összege 360∘, létezik három egymást követő csúcsa, például R,S és P úgy, hogy az ezeknél fekvő szögekre QPS∢+PSR∢≧180∘ és PSR∢+SRQ∢≧180∘ teljesül. Ekkor található olyan X pont a négyszögben, amellyel az XRSP négyszög paralelogramma (5. ábra). Az XRSP paralelogramma így az eredeti háromszögben fekszik, ezért (1) alapján a területe legfeljebb 1/2. A PSR háromszög területe az XRSP paralelogramma területének a fele, tehát legfeljebb 1/4. Ezzel a feladatot megoldottuk.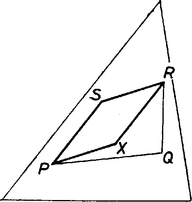
 
 
5. ábra
 

 

 Végső Viktor (Nyíregyháza, Vásárhelyi P. Ép. Szki., I. o. t.) és
 Czirók András (Miskolc, Földes F. Gimn., II. o. t.)
 dolgozata alapján