Kezdőlap


Feladat:	Gy.2522	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Szabó Zsuzsanna
Füzet:	1989/október, 306. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Magasságvonal, Szögfelező egyenes, Körülírt kör, Diszkusszió, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1988/december: Gy.2522

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a feladatot megoldottnak. Az $A B C$ háromszög szögei legyenek $2 α, 2 β$ és $2 γ$ , a belső szögfelezőknek a háromszög köré írt körrel való metszéspontjait jelölje rendre $A_{1}, B_{1}$ és $C_{1}$ , a külső szögfelezők és a kör metszéspontjai pedig 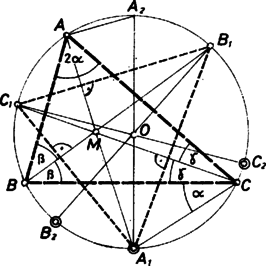$A_{2}, B_{2}$ és $C_{2}$ .

Tudjuk, hogy egy háromszög egyik csúcsához tartozó külső és belső szögfelezők egymásra merőlegesek, azaz

A_{1} A A_{2} ∢ = B_{1} B B_{2} ∢ = C_{1} C C_{2} ∢ = 90^{\circ}

. Így ‐ Thalész tétele szerint ‐

A_{1} A_{2}, B_{1} B_{2}

és

C_{1} C_{2}

a körülírt körnek átmérői. A kerületi szögek tétele alapján:

\begin{matrix} B C A_{1} ∢ = B A A_{1} ∢ = α, \\ B_{1} A_{1} C ∢ = B_{1} B C ∢ = β . \end{matrix}

Ezért a

B_{1} A_{1} C

és a

C_{1} C A_{1} (= C_{1} C B + B C A_{1})

szögek összege

β + γ + α = 90^{\circ}

, azaz a

C C_{1}

egyenes merőleges az

A_{1} B_{1}

egyenesre. Ugyanígy láthatjuk be, hogy

A A_{1}

és

B_{1} C_{1}

, valamint

B B_{1}

és

A_{1} C_{1}

is egymásra merőleges egyenesek, vagyis az

A_{1} B_{1} C_{1}

háromszög magasságvonalai megegyeznek az

A B C

háromszög belső szögfelezőivel.
Ezek alapján a szerkesztés már könnyen elvégezhető. Ha adottak pl. az

A_{1}, B_{2}

és

C_{2}

pontok, akkor megszerkesztjük a rajtuk átmenő kört. A

B_{2}

és

C_{2}

pontokat a kör középpontjára tükrözve megkapjuk

B_{1}

-et és

C_{1}

-et, végül az

A_{1} B_{1} C_{1}

háromszög magasságvonalai kimetszik a körből a keresett

A, B, C

pontokat. Az így szerkesztett háromszög az előzőekben leírtak alapján eleget is tesz a feltételeknek.
A feladatnak általában egy megoldása van. Nincs megoldás, ha az

A_{1}, B_{2}, C_{2}

pontok egy egyenesre esnek, vagy ha az

A_{1} B_{2} C_{2}

háromszög valamelyik szöge derékszög. Ez utóbbi esetben ugyanis az

A_{i}, B_{i}, C_{i}

pontok némelyike egybeesne, ami nem lehetséges.

Szabó Zsuzsanna (Mosonmagyaróvár, Haller J. Ált. Isk., 8. o. t.)
dolgozata alapján