| Feladat: | Gy.2520 | Korcsoport: 14-15 | Nehézségi fok: átlagos |
| Füzet: | 1989/szeptember, 261. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Indirekt bizonyítási mód, Négyzetrács geometriája, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1988/december: Gy.2520 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Képzeljük a négyzetrácsot végtelen sakktáblának, és helyezzünk el rajta 8 db -es dominót az ábrán látható módon. Megmutatjuk, hogy ekkor a megmaradó részt nem lehet -es dominókkal lefedni. 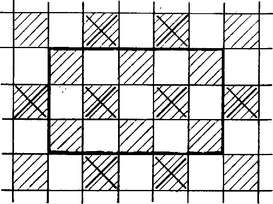 Tegyük fel, hogy mégis sikerült a lefedés, és nevezzük jónak azokat az -es dominókat, amelyek a bekeretezett téglalap belsejében helyezkednek el. Vegyük észre, hogy a téglalap fehér mezőit csak ilyen jó dominók fedhetik le, és mivel minden dominó egy fehér és egy fekete mezőt takar, a jó dominók száma szükségképpen 7. Ez viszont lehetetlen, mivel a téglalap szabad mezőjén legfeljebb 6 dominó fér el. Megjegyzés. Több dolgozat szerint elég annyit biztosítani, hogy a végtelen sakktáblán úgy helyezzük el a véges sok -es dominót, hogy több essék pl. fekete mezőre, mint fehérre. Ekkor ugyanis ‐ mint írták ‐ kevesebb fekete mező marad fedetlen, mint fehér, és így nem lehetséges a lefedés. Ez, és minden ehhez hasonló okoskodás hibás. Először is, akárhogy helyezünk el a síkon véges sok -es dominót, a maradék fehér és fekete mezők továbbra is párba állíthatók, tehát ,,ugyanannyian'' vannak. Másrészt könnyen meggyőződhetünk arról, hogy tetszőleges számú fekete mezőt lefedhetünk ‐ például mindegyiket egyetlen sorból ‐ úgy, hogy a fedetlen rész továbbra is lefedhető legyen -es dominókkal. |