Kezdőlap


Feladat:	Gy.2516	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Barabás Gyula
Füzet:	1989/december, 455 - 457. oldal		PDF \| MathML
Témakör(ök):	Beírt alakzatok, Terület, felszín, Négyszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1988/november: Gy.2516

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az adott pontok helyzetétől függően több esetet kell megkülönböztetnünk: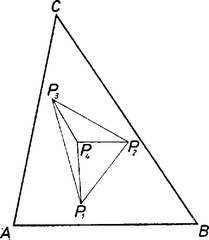
Ha az adott pontok között van három, amelyek egy egyenesbe esnek, akkor az ezek által meghatározott elfajult háromszög területe $0,$ tehát ekkor az állítás igaz.

1. ábra

Ha a négy pont között van egy, amelyik a másik három által alkotott háromszög belsejében helyezkedik el, akkor ‐ az 1. ábra jelöléseit használva:

\begin{matrix} T_{P_{1} P_{2} P_{4}} + T_{P_{2} P_{3} P_{4}} + T_{P_{1} P_{3} P_{4}} = T_{P_{1} P_{2} P_{3}} ≦ T_{A B C} = 1. \end{matrix}

Ebből pedig nyilván következik, hogy a

P_{1} P_{2} P_{4}

P_{2} P_{3} P_{4}

és

P_{1} P_{3} P_{4}

háromszögek mindegyikének a területe nem lehet

1 / 3

-nál nagyobb; ebben az esetben is igaz a feladat állítása.
Hátra van még annak az esetnek a vizsgálata, amikor az adott pontok egy konvex négyszöget határoznak meg. A bizonyítás során két segédtételt fogunk használni :

(1) Minden konvex négyszögbe beírható olyan paralelogramma, amelynek három csúcsa megegyezik a négyszög valamely három csúcsával.

2. ábra

Bizonyítás. Ha a négyszög maga is paralelogramma, akkor készen vagyunk. Ha a négyszög nem paralelogramma, akkor feltehetjük, hogy az

A B

és

C D

oldalai az

M

pontban metszik egymást (2. ábra), ahol például

A

és

D,

illetve

M

B C

egyenes különböző oldalain helyezkednek el. Válasszuk ki

A

és

D

közül azt, amelyiknek

B C

-től mért távolsága a kisebb; feltehetjük, hogy esetünkben ez éppen az

A

pont. Húzzunk

A

-n keresztül párhuzamost

B C

-vel, e párhuzamos a

C D

egyenest

E

-ben metszi. Feltevéseinkből következik, hogy

E

C D

szakaszon van, így a keletkezett

A B C E

trapézt az

A B C D

négyszög tartalmazza. Azt is tudjuk, hogy

B C < A E

, hiszen

M

B C

-nek

A E

-vel ellentétes oldalán van. Tehát a

C

-n át

A B

-vel húzott párhuzamos egy

F

belső pontban metszi az

A E

szakaszt. Vagyis az

A B C F

paralelogrammát tartalmazza az

A B C E

trapéz, és így az

A B C D

négyszög is. Ezzel az (1) segédtételt beláttuk.

(2) Egy háromszögben elhelyezkedő paralelogramma területe legfeljebb fele a háromszög területének.
Ennek az állításnak a bizonyítása megtalálható a 2524. gyakorlat megoldásában, lapunk szeptemberi számának 263. oldalán.
Ezek után a harmadik eset bizonyítása már egyszerű : Az 1. segédtétel alapján kiválasztható a négy pont közül három, melyek egy, a háromszögben fekvő paralelogrammának csúcsai. A 2. segédtétel szerint ennek a paralelogrammának a területe legfeljebb

1 / 2

. Egy paralelogramma három csúcsa által alkotott háromszög területe azonban pontosan a paralelogramma területének fele, esetünkben legfeljebb

1 / 4

Barabás Gyula (Nyíregyháza, Krúdy Gy. Gimn., II. o. t.) dolgozata alapján