Kezdőlap


Feladat:	Gy.2515	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bende Z.
Füzet:	1989/október, 305 - 306. oldal		PDF \| MathML
Témakör(ök):	Trapézok, Paralelogrammák, Érintőnégyszögek, Ellipszis, mint mértani hely, Gyakorlat
Hivatkozás(ok):	Feladatok: 1988/november: Gy.2515

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tudjuk, hogy egy konvex négyszög pontosan akkor érintőnégyszög, ha szemközti oldalainak hosszúságösszege megegyezik. Tehát $A B C D$ pontosan akkor érintőnégyszög, ha 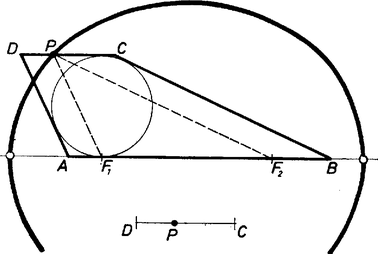$A B + C D = A D + B C$ .

Legyen

P

C D

szakasz kiszemelt pontja. Az

F_{1}, F_{2}

pontokat úgy vegyük fel az

A B

, ill.

B A

félegyenesen, hogy

A F_{1} = D P

és

F_{2} B = P C

teljesüljön. Ekkor (

C D

tetszőleges helyzetében) az

A F_{1} P D

és az

F_{2} B C P

négyszögek paralelogrammák, tehát

A D + B C = F_{1} P + F_{2} P

. Ha

A B C D

érintőnégyszög, akkor

A B + C D = A D + B C = F_{1} P + F_{2} P

, vagyis a

P

pontnak

F_{1}

és

F_{2}

pontoktól való távolságainak az összege állandó, azaz a

P

pont rajta van az

F_{1}

és

F_{2}

fókuszú,

A B + C D

nagytengelyű ellipszisen. Ennek az ellipszisnek minden olyan pontja, amelyik nincs rajta az

A B

egyenesen, rendelkezik a kívánt tulajdonsággal. Ha ugyanis

P'

az ellipszisnek nem az

A B

egyenesen levő pontja, akkor a

P'

-n átmenő,

A B

-vel párhuzamos egyenesen léteznek olyan

D'

és

C'

pontok, amelyekre

D' P' = A F_{1}

és

P' C' = F_{2} B

. Minden ilyen négyszög érintőtrapéz, hiszen

A B + C' D' = P' F_{1} + P' F_{2} = A D' + B C'

.
Tehát a

C D

szakasz egy rögzített pontja ellipszisen mozog, és két pont kivételével annak minden pontjába eljut.