Feladat: Gy.2501 Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1989/április, 167 - 168. oldal  PDF  |  MathML 
Témakör(ök): Téglalapok, Térelemek és részeik, Tetraéderek, Gyakorlat
Hivatkozás(ok):Feladatok: 1988/szeptember: Gy.2501

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha az ABCD tetraédert az S sík téglalapban metszi, akkor S-nek a tetraéder négy élével van közös pontja; ez azt jelenti, hogy S-nek mindkét oldalán két-két tetraédercsúcs helyezkedik el.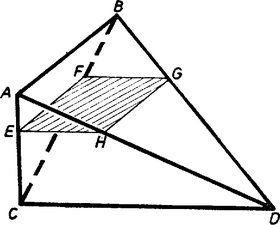

 
 

Tegyük fel, hogy a síkmetszet az EFGH téglalap, melynek csúcsai rendre az AC,CB,BD,DA éleken vannak (lásd az ábrát). Megmutatjuk, hogy a tetraéder AB éle párhuzamos az EF és HG szakaszokkal. Tekintsük az ABC,ABD és EFGH síkokat; e síkok páronkénti metszésvonalai rendre AB,EF és HG. Ismeretes, hogy három, egymást páronként metsző sík metszésvonalai vagy egy ponton mennek át, vagy pedig párhuzamosak (lásd pl. Geometriai feladatok gyűjteménye I., 1703. feladat). Esetünkben tudjuk, hogy EF és HG párhuzamosak, tehát AB is csak ezekkel párhuzamos lehet. Ugyanígy kapjuk, hogy CD,FG és EH is párhuzamosak. Az EF és FG szakaszok viszont egymásra merőlegesek, ezért a velük párhuzamos AB és CD élek is merőlegesek egymásra. Tehát, ha egy tetraédernek van téglalap alakú síkmetszete, akkor a tetraédernek van két egymásra merőleges kitérő éle.
Belátjuk, hogy ez a feltétel elégséges is, azaz: ha egy tetraéder két szemközti éle merőleges egymásra, akkor a tetraédernek van téglalap alakú síkmetszete. Tegyük fel, hogy az ABCD tetraéder AB és CD éle egymásra merőleges. Messük el a tetraédert egy olyan EFGH síkkal, amelyik AB-vel és CD-vel is párhuzamos. (Ilyen sík valóban létezik; pontosan azok a síkok felelnek meg, amelyek merőlegesek a két egyenes normáltranszverzálisára.) Tekintsük ismét az ABC,ABD és EFGH síkok páronkénti metszésvonalait, AB-t, EF-et és GH-t. Ha EF és GH metszené egymást, akkor ezen a metszésponton AB-nek is át kellene mennie; ez azonban lehetetlen, hiszen akkor EF és GH metszéspontja az AB-vel párhuzamos EFGH síkban lenne. Tehát EF és GH egymással is és AB-vel is párhuzamosak. Ugyanígy kapjuk, hogy CD,FG és EH párhuzamosak. Vagyis az EFGH négyszög paralelogramma, mivel szemközti oldalai párhuzamosak. EF és FG szöge megegyezik a velük párhuzamos AB és CD szögével, vagyis 90∘. Ez éppen azt jelenti, hogy az EFGH paralelogramma téglalap.
 

Tehát pontosan azoknak a tetraédereknek van téglalap alakú síkmetszetük, amelyeknek van két egymásra merőleges kitérő élük.
 

Megjegyzések. 1. Bizonyításunk második részéből az is kiderült, hogy ha egy tetraédert két kitérő élével párhuzamos síkokkal metszünk, akkor a síkmetszet paralelogramma. Ez azt jelenti, hogy minden tetraédernek van paralelogramma alakú síkmetszete.
 

2. Ha az E,F,G,H pontokat úgy választjuk a tetraéder AC,BC,BD és AD élein, hogy valamely λ számmal AE=λ⋅AC,AH=λ⋅AD,BF=λ⋅BC és BG=λ⋅BD teljesüljön, akkor az AEH és ACD,BFG és BCD,CEF és CAB,DHG és DAB háromszögpárok hasonlóak, hiszen megegyezik két-két oldaluk aránya és az azok által bezárt szög. Ezért EH=FG=λ⋅CD és EF=HG=(1-λ)⋅AB. Másrészt például EH és FG párhuzamosak is ‐ mindkettő párhuzamos CD-vel ‐, tehát az EFGH négyszög paralelogramma. Ha λ-t úgy választjuk, hogy EH=EF teljesüljön, azaz λ=ABAB+CD, akkor az EFGH paralelogramma rombusz. Tehát minden tetraédernek van rombusz alakú síkmetszete.
 

3. Az előző pontban leírtakból, valamint feladatunk eredményéből következik, hogy ha egy tetraédernek van téglalap alakú síkmetszete, akkor négyzet alakú síkmetszete is van.