Kezdőlap


Feladat:	Gy.2499	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Mikulás Imre
Füzet:	1989/április, 165 - 167. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Trigonometriai azonosságok, Hozzáírt körök, Hossz, kerület, Diszkusszió, Háromszögek szerkesztése, Körérintési szerkesztések, Szögfüggvények, síkgeometriai számítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1988/szeptember: Gy.2499

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tekintsük a feladatot megoldottnak. Az $A B C$ háromszög $B C$ oldalához hozzáírt kör érintse a háromszög oldalegyeneseit a $D, F, E$ pontokban, az $A C$ oldalhoz hozzáírt kör pedig ezt az oldalt a $G$ pontban (1. ábra).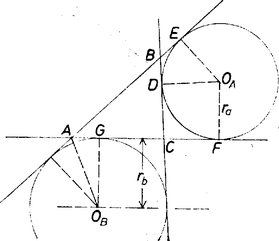

1. ábra

Tudjuk, hogy egy külső pontból a körhöz húzott két érintőszakasz egyenlő, ezért

B D = B E

és

C D = C F

; tehát az

A E = A B + B E

és az

A F = A C + C F

szakaszok összege megegyezik az

A B C

háromszög kerületével. De

A E = A F

, tehát mindkét szakasz hosszúsága megegyezik a háromszög félkerületével,

s

-sel. Ezt felhasználva már el tudjuk végezni a szerkesztést:
Felveszünk egy

r_{a}

sugarú kört és a kerületén tetszőlegesen kijelöljük az

F

pontot. Megszerkesztjük a kör

F

-beli érintőjét és erre felmérjük az

F A = s

távolságot, ami adott. Ezután

A

-ból megszerkesztjük a körhöz a másik érintőt (ez éppen a háromszög

A B

oldalegyenese). A másik hozzáírt kör érinti az

A F

és az

A B

egyeneseket, sugara pedig adott, tehát ezt a kört is meg tudjuk szerkeszteni. (A kör középpontja rajta van az

F A B

szög külső szögfelezőjén, és az

A B

egyenestől

r_{b}

távolságra lévő párhuzamos egyenesen is.) Végül a

B C

egyenest úgy kapjuk, hogy megszerkesztjük a két kör

A F

-től különböző közös belső érintőjét. (Két kör közös érintőjének szerkesztése megtalálható pl. a Geometriai feladatok gyűjteménye I. 633. feladatában.) A leírtakból következik, hogy az így szerkesztett

A B C

háromszög egyik hozzáírt körének sugara

r_{a}

, egy másik hozzáírt körének sugara

r_{b}

, kerülete pedig

2 A F = 2 s

, vagyis a háromszög megfelel a követelményeknek.
A szerkesztés pontosan akkor végezhető el, ha a

G

pont az

A F

szakasz belső pontja. Ebben az esetben 1 megoldás van, egyébként pedig nincs megoldás. (A II. megoldásban megmutatjuk, hogy

G

pontosan akkor belső pontja az

A F

szakasznak, ha

r_{a} \cdot r_{b} < s^{2}

II. megoldás. Használjuk a 2. ábra jelöléseit.

2. ábra

A T_{1} O_{1}

és

B T_{2} O_{2}

derékszögű háromszögeket meg tudjuk szerkeszteni, hiszen ismert két-két befogójuk (

A T_{1} = B T_{2} = s, O_{1} T_{1} = r_{a}

és

O_{2} T_{2} = r_{b}

). Az

A O_{1}

és a

B O_{2}

egyenesek viszont szögfelezők az

A B C

háromszögben, tehát

O_{1} A T_{1} ∢ = \frac{α}{2}

és

O_{2} B T_{2} ∢ = \frac{β}{2}

. Ezért a szerkesztendő

A B C

háromszög két szöge megszerkeszthető az

A T_{1} O_{1}

és a

B T_{2} O_{2}

háromszögek segítségével. Így tudunk szerkeszteni

A B C

-hez hasonló

A' B' C'

háromszöget, majd ezt a kerületek arányában nagyítva/kicsinyítve kapjuk az

A B C

háromszöget. Az így szerkesztett háromszög nyilván eleget tesz a feltételeknek.
A szerkeszthetőségnek az a feltétele, hogy

α + β 180^{\circ}

-nál kisebb (és természetesen pozitív) legyen. Ez ekvivalens a

0^{\circ} < \frac{α}{2} + \frac{β}{2} < 90^{\circ}

feltétellel; azaz pontosan akkor létezik megoldás, ha

tg (\frac{α}{2} + \frac{β}{2}) > 0

. Mivel

tg \frac{α}{2} = \frac{r_{a}}{s}, tg \frac{β}{2} = \frac{r_{b}}{s}

, ezért

\begin{matrix} tg (\frac{α}{2} + \frac{β}{2}) = \frac{tg \frac{α}{2} + tg \frac{β}{2}}{1 - tg \frac{α}{2} \cdot tg \frac{β}{2}} = \frac{\frac{r_{a}}{s} + \frac{r_{b}}{s}}{1 - \frac{r_{a} \cdot r_{b}}{s^{2}}} . \end{matrix}

Ez a tört akkor pozitív, ha a nevezője pozitív, tehát a megszerkesztendő háromszög pontosan akkor létezik, ha

s^{2} > r_{a} \cdot r_{b}

. Ekkor a feladatnak 1 megoldása van, egyébként pedig nincs megoldása.

Mikulás Imre (Nyíregyháza, Krúdy Gyula Gimn., II. o. t.)
dolgozata alapján